括号序列的性质总结

题目链接 =======> 传送门

合法括号序列的性质

• 左、右括号的数量相等。

• 任意前缀的左括号数量必须大于等于右括号数量。

最少需要添加括号的数量

• 为了尽可能添加少的括号，所以添加的左、右括号不会出现如同$"()"$的形式。

• 从前往后遍历，当前前缀中，若左括号的数量小于右括号的数量，则需要添加对应数量的左括号，若遍历结束后左括号数量大于右括号，则需要添加对应数量的右括号。

通过上面的分析，我们发现，我们的分析对题目好像没有什么卵用

本题分析——添加括号的方案：

• 左括号与右括号添加的位置方案是相互独立的，不会相互影响，即使左、右括号添加在同一个间隙，因为不能存在$"()"$的形式，此处只能为类似$"))(("$的一种形式，故总的方案数等于左括号的方案数 $×$ 右括号的方案数。

• 单独考虑添加左括号，若以右括号为分割点， 将整个序列进行分割，因为分割后的子串中均为左括号， 添加任意数目的左括号方案数均为一种，那么此时，我们仅需考虑添加不同数量的左括号的方案数即可。

• 右括号同理，翻转字符串和左右括号即可对称地做一遍。

第一次calc得到 加入最少的左括号使得任意前缀 左括号数量 $>=$ 右括号数量 那么前缀为整个字符串的时候也满足 左括号数量 $>=$ 右括号数量。第二次枚举可以得到加入最少的右括号使得任意后缀 右括号数量 $>=$ 左括号数量，对于整个字符串来看 有左括号 $>=$ 右括号 右括号 $>=$ 左括号 推出右括号数量 $=$ 左括号数量。

动态规划

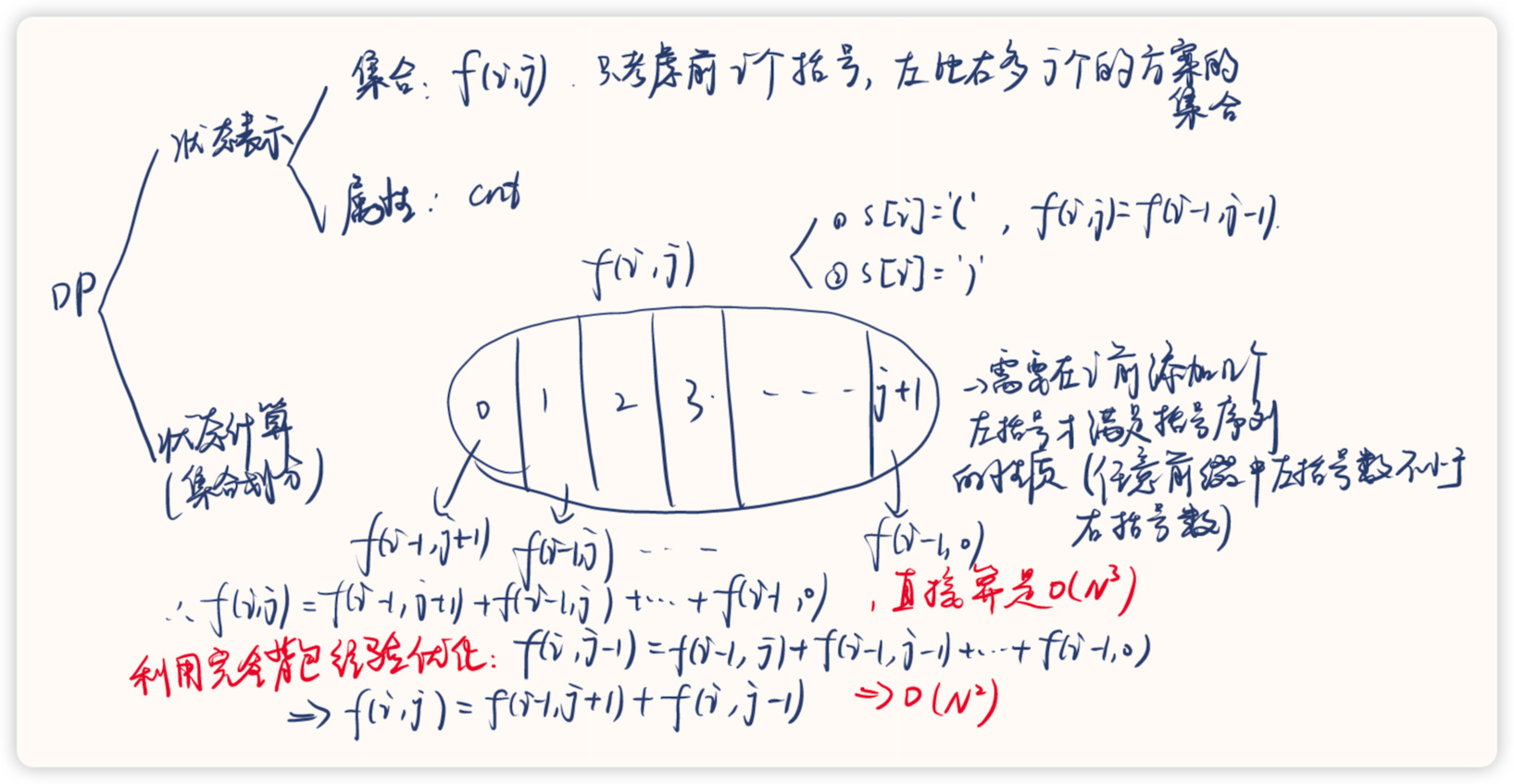
AC代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 5010, mod = 1e9 + 7;
char s[N];
LL f[N][N];
int n;

LL calc(){
	memset(f, 0, sizeof f);
	f[0][0] = 1;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n; j++){
			if(s[i] == '(') f[i][j] = f[i - 1][j - 1];
			else{
				f[i][0] = (f[i - 1][1] + f[i - 1][0]) % mod;  //特判一下
				f[i][j] = (f[i - 1][j + 1] + f[i][j - 1]) % mod;
			}
		}
	}
	for(int i = 0; i <= n; i++)
		if(f[n][i]) return f[n][i];
	return -1;
}

void solve(){
	scanf("%s", s + 1);
	n = strlen(s + 1);
	LL lans = calc();
	reverse(s + 1, s + 1 + n);
	for(int i = 1; i <= n; i++){
		if(s[i] == '(') s[i] = ')';
		else s[i] = '(';
	}
	LL rans = calc();
	printf("%lld\n", lans * rans % mod);
}

int main(){
	int T = 1;
	// scanf("%d", &T);
	while(T -- ){
		solve();
	}

	return 0;
}