牛客寒假集训营第二场补题

yuanheci 2023年01月19日 181次浏览

1、A题 《Tokitsukaze and a+b=n (easy)》

题目描述：

easy 与 medium 的唯一区别是输入的数据范围。

TokitsukazeTokitsukaze 有一个整数 nn， 以及 22 个区间 [L1,R1][L_1,R_1] , [L2,R2][L_2,R_2]。

她想知道有多少种选法，满足：从第一个区间选择一个整数 a(L1≤a≤R1)a (L1≤a≤R1)，从第二个区间选择一个整数 b(L2≤b≤R2)b (L2≤b≤R2)，使得 a+b=na+b=n。

对于两种选法，若 aa, bb 中有任意一个数不同，则算作不同的选法。

输入描述：

第一行包含一个整数 T(1≤T≤5)T (1≤T≤5)，表示测试数据组数。

对于每组测试数据：

第一行包含一个整数 n(1≤n≤2∗105)n(1≤n≤2 * 10^5)。

第二行包含两个整数 L1,R1(1≤L1≤R1≤105)L_1, R_1 (1≤L1≤R1≤10^5)。

第三行包含两个整数 L2,R2(1≤L2≤R2≤105)L_2, R_2 (1≤L2≤R2≤10^5)。

输出描述：

对于每组测试数据，输出一个整数表示答案。

示例1

输入：
4
5
3 5
1 4
100000
1 100000
1 100000
200000
1 100000
1 100000
114
514 1919
8 10

输出：
2
99999
1
0

说明：

第一组测试数据：共有 22 种选法，分别是 (3+2)(3+2), (4+1)(4+1)。

本题虽然是个签到题，但是赛时做的方法不够简单，这里记录一下比较好的做法，没必要用hash。

AC代码

#include <bits/stdc++.h>
using namespace std;

int n; 
int ans;

int main(){
	int T;
	scanf("%d", &T);
	while(T -- ){
		scanf("%d", &n);
		int l1, r1, l2, r2;
		scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
		ans = 0;
		for(int i = l1; i <= r1; i++){
			int x = n - i;
            //直接判断在不在区间中即可，这样就省去了一维
			if(x >= l2 && x <= r2) ans++;  
		}	
		printf("%d\n", ans);
	}
	
	return 0;
}

2、B题 《Tokitsukaze and a+b=n (medium)》

本题与AA题的区别是区间范围扩大到了1e91e9

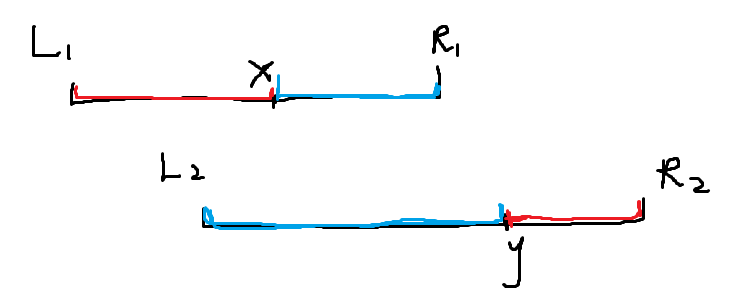
比赛时的做法是根据两个区间二分来做，对于一个区间二分查找一个 xx 能够满足在另一个区间中存在 yy 使得 x+y=nx + y = n，yy 也通过二分在另一个区间中进行查找，注意因为是连续区间，所以没有重复的数。

如果找到了这样的xx, yy，那么令 x+1x + 1, y−1y - 1 就也是一对满足条件的数，同理 x−1x - 1, y+1y + 1 也是。

该算法的时间复杂度为O(logn∗logn),n=1e9O(logn * logn), n = 1e9

33-1674136503819

所以

ans=ans+min(l−l1+1,r2−y+1);ans = ans + min(l - l_1 + 1, r_2 - y + 1);
ans=ans+min(r1−l+1,y−l2+1);ans = ans + min(r_1 -l + 1, y - l_2 + 1);

注意对于边界情况也特殊讨论一下，赛中临时魔改了一下二分，竟然真的过了。。。

关键就是，当二分指针移出最左边以及移出最右边时都是不存在的情况。

AC代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
int n;
LL l1, r1, l2, r2;
LL ans;
LL y;

int check(LL x){
	y = n - x;
	LL l = l2 - 1, r = r2 + 1;
	while(l < r){
		LL mid = l + r >> 1;
		if(mid >= y) r = mid;
		else l = mid + 1;
	}
	if(l == y) return 1;
	else if(l == l2 - 1) return 2;
	else if(l == r2 + 1) return 3;
	return 0;
}

int main(){
	int T;
	scanf("%d", &T);
	while(T -- ){
		scanf("%d", &n);
		scanf("%lld%lld%lld%lld", &l1, &r1, &l2, &r2);
		LL l = l1 - 1, r = r1 + 1;
		while(l < r){
			LL mid = l + r >> 1;
			int z = check(mid);
			if(z == 1) {
				l = mid;
				break;
			}
			else if(z == 2) r = mid - 1; 
			else if(z == 3) l = mid + 1;
		}
		ans = 0;
		if(l == l1 - 1 || l == r1 + 1) ans = 0;
		else{
			ans += min(l - l1 + 1, r2 - y + 1);
			ans += min(r1 -l + 1, y - l2 + 1);
		}
		printf("%lld\n", max(1LL* 0, ans - 1));
	}
	
	return 0;
}

更好的做法：推公式法

根据 aa 的取值范围 [L1,R1][L_1,R_1]，我们求出能满足 a＋b=na＋b= n 的 bb 的范围是 [n−R1,n−L1][n - R_1,n - L_1]，但是合法的 bb 的范围是[L2,R2][L_2, R_2]。所以答案是区间 [n−L1,n−R1][n - L_1, n - R_1] 与 [L2,R2][L_2, R_2] 取交后的区间长度。
区间取交的区间长度可以这么计算：

两个区间 [a,b][a,b], [c,d][c, d]相交后的结果为：[max(a,c),min(b,d)][max(a, c), min(b, d)]；

两个区间 [a,b][a,b]，[c,d][c,d]取交的区间长度为： max(0,min(b,d)−max(a,c)+1)max(0, min(b,d) - max(a,c) + 1)；

注意 min(b,d)−max(a,c)min(b, d) - max(a, c) 可能是负的，表示两个区间没有交集，因此最终答案要和 00 取 maxmax。

AC代码：

#include <bits/stdc++.h>
using namespace std;

int n;
int l1, r1, l2, r2;
int ans;

int main(){
	int T;
	scanf("%d", &T);
	while(T -- ){
		scanf("%d", &n);
		scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
		int a = n - r1, b = n - l1;
		int c = l2, d = r2;
		printf("%d\n", max(0, min(b, d) - max(a, c) + 1)); 
	}
	
	return 0;
}

3、C题 《Tokitsukaze and a+b=n (hard)》

题目描述

TokitsukazeTokitsukaze 有一个整数 nn， 以及 mm 个区间 [L,R][L,R]。

她想知道有多少种选法，满足：从 mm 个区间中选择两个区间 [Li,Ri][L_i,R_i], [Lj,Rj](i≠j)[L_j,R_j](i \ne j)，并从第一个区间选择一个整数 a(Li≤a≤Ri)a (L_i \leq a \leq R_i)，从第二个区间选择一个整数 b(Lj≤b≤Rj)b (L_j \leq b \leq R_j)，使得 a+b=na+b=n。

对于两种选法，若 ii, jj , aa, bb 中有任意一个数不同，则算作不同的选法。

由于答案可能很大，请输出对 998244353998 244 353 取模后的结果。

输入描述

第一行包含两个整数 n,m(2≤n,m≤4⋅105)n, m (2≤n,m≤4⋅10^5)。

接下来 mm 行，每行包含两个整数 L,R(1≤L≤R≤2∗105)L, R (1≤L≤R≤2 * 10^5)。

输出描述

输出一个整数表示答案对 998 244 353998 244 353 取模后的结果。

示例

输入：
5 3
1 3
2 4
3 5

输出：
12

分析

Screenshot_20230119_172013

时间复杂度 O(n+m)O(n + m)

PS:PS: 本题还可以使用树状数组 // 线段树等数据结构进行区间求和。

AC代码

差分版本

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 4e5 + 10, mod = 998244353;
LL c[N];
LL tot, cnt1;
int n, m;

int main(){
	scanf("%d%d", &n, &m);
	//计算差分
	for(int i = 0; i < m; i++){
		int l, r;
		scanf("%d%d", &l, &r);
		c[l]++, c[r + 1]--;
		cnt1 = (cnt1 + max(0, min(n - l, r) - max(n - r, l) + 1)) % mod;
	} 
	for(int i = 1; i <= n; i++) c[i] = (c[i] + c[i - 1]) % mod;
	
	for(int i = 1; i <= n ; i++){
		tot = (tot + c[i] * c[n - i] % mod) % mod;
	}

	printf("%lld\n", (tot - cnt1 + mod) % mod);
	
	return 0;
}

树状数组版本

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 4e5 + 10, mod = 998244353;
LL tr[N];
LL tot, cnt1;
int n, m;

int lowbit(int x){
	return x & -x;
} 

void add(int x, int c){
	for(int i = x; i <= n; i += lowbit(i)){
		tr[i] += c;
	}
}

LL query(int x){
	LL ans = 0;
	for(int i = x; i; i -= lowbit(i)){
		ans += tr[i];
	} 
	return ans;
}

int main(){
	scanf("%d%d", &n, &m); 
	for(int i = 0; i < m; i++){
		int l, r;
		scanf("%d%d", &l, &r);
		add(l, 1), add(r + 1, -1);
		cnt1 = (cnt1 + max(0, min(n - l, r) - max(n - r, l) + 1)) % mod;
	} 
	
	for(int i = 1; i <= n ; i++){
		tot = (tot + query(i) * query(n - i) % mod) % mod;
	}

	printf("%lld\n", (tot - cnt1 + mod) % mod);
	
	return 0;
}

线段树版本

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 4e5 + 10, mod = 998244353;
LL tot, cnt1;
int n, m;

struct Node{
	int l, r;
	LL sum;
}tr[N * 4];

void pushup(int u){
	tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u, int l, int r){
	tr[u] = {l, r, 0};
	if(l == r) return;
	int mid = l + r >> 1;
	build(u << 1, l, mid);
	build(u << 1 | 1, mid + 1, r);
} 

void modify(int u, int x, int c){
	if(tr[u].l == x && tr[u].r == x) tr[u].sum += c;
	else{
		int mid = tr[u].l + tr[u].r >> 1;
		if(x <= mid) modify(u << 1, x, c);
		else modify(u << 1 | 1, x, c);
		pushup(u);
	}
}

LL query(int u, int l, int r){
	if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
	else{
		LL ans = 0;
		int mid = tr[u].l + tr[u].r >> 1;
		if(l <= mid) ans = (ans + query(u << 1, l, r)) % mod;
		if(r > mid) ans = (ans + query(u << 1 | 1, l, r)) % mod;
		return ans;
	}
}

int main(){
	scanf("%d%d", &n, &m);
	build(1, 1, 200010);  //注意这里要开到大于2e5, 否则会溢出 
	for(int i = 0; i < m; i++){
		int l, r;
		scanf("%d%d", &l, &r);	
		modify(1, l, 1), modify(1, r + 1, -1);
		cnt1 = (cnt1 + max(0, min(n - l, r) - max(n - r, l) + 1)) % mod;
	} 
	
	for(int i = 1; i <= n; i++){
		tot = (tot + query(1, 1, i) * query(1, 1, n - i) % mod) % mod;
	}

	printf("%lld\n", (tot - cnt1 + mod) % mod);
	
	return 0;
}

4、D题 《Tokitsukaze and Energy Tree》

题目描述

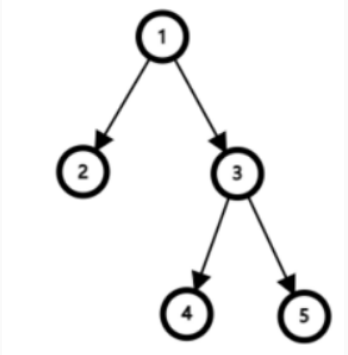
TokitsukazeTokitsukaze 有 nn 个节点的有根能量树，根为 11。最开始，树上每个节点的能量都是 00。

现在 TokitsukazeTokitsukaze 有 nn 个能量球，第 ii 个能量球拥有 viv_i​ 能量。她想把这 nn 个能量球分别放置在能量树的每个节点上，使能量树的每个节点都恰好有一个能量球。

TokitsukazeTokitsukaze 每次只能放置一个能量球，所以她将进行 nn 次操作。每一次操作，她会选择一个能量球，再选择一个没有能量球的能量树节点 xx，把刚刚选择的能量球放置在节点 xx 上。在这之后，TokitsukazeTokitsukaze 能获得以 xx 为根的子树中的所有能量球的能量 (包括节点 xx 的能量球能量)。

在放置完所有能量球后，TokitsukazeTokitsukaze 可能获得的总能量最多是多少？

输入描述：

第一行包含一个整数 n(1≤n≤2⋅105)n (1≤n≤2⋅10^5)。

第二行包含 n−1n−1 个整数 f2,f3,…,fn(1≤fi≤i−1)f2,f3,…,fn(1≤fi≤i−1)，表示节点 ii 的父亲是 fif_i。

第三行包含 nn 个整数 v1,v2,…,vn(1≤vi≤105)v_1,v_2,…,v_n (1≤v_i≤105)，分别表示能量球的能量。

输出描述：

输出一个整数，表示 TokitsukazeTokitsukaze 可能获得的最多总能量。

示例1

image-20230119131555457

输入：
5
1 1 3 3
1 1 2 2 3

输出：
22

分析

经典结论： 两个向量内部允许任意重排，则点积最大方法为都升序排序。

可以发现当第 ii 个能量球放置在节点 xx 时，它的贡献为：节点 11 到节点 xx 的高度 hxh_x。能量球的能量 viv_i 。于是我们可以贪心来算，求出高度 hh 后，分别对高度 hh 和能量 vv 排序，之后大的乘大的，再全部加起来即可。

求树中每个结点的高度（深度）可以用 dfsdfs

AC代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 2e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], idx;
int dep[N], v[N];
int n;

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

//计算树中每个结点的深度, 记根结点深度为 1
void dfs(int u, int d){
    dep[u] = d;
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        dfs(j, d + 1);
    }
}

int main(){
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for(int i = 2; i <= n; i++){
        int p;
        scanf("%d", &p);
        add(p, i);
    }
    for(int i = 1; i <= n; i++) scanf("%d", &v[i]);
    dfs(1, 1);
    sort(dep + 1, dep + 1 + n);
    sort(v + 1, v + 1 + n);
    
    LL ans = 0;
    for(int i = 1; i <= n; i++) ans += 1LL* dep[i] * v[i];
    printf("%lld\n", ans);
    
    return 0;
}

5、F题《Tokitsukaze and Gold Coins (easy)》

题目描述

easy 与 hard 的唯一区别是输出内容。

TokitsukazeTokitsukaze 喜欢 RuneFactoryRune Factory 系列。

在游戏中有一个 n×3n×3 的迷宫，迷宫的起点是 (1,1)(1,1)，迷宫的终点是 (n,3)(n,3)，每个格子都有一条向下和一条向右的单向道路，也就是说如果你当前站在 (x,y)(x,y)，你只能前往 (x+1,y)(x+1,y) 或者 (x,y+1)(x,y+1)。

在迷宫的起点设有离开迷宫的出口，玩家可以通过出口安全的离开迷宫。

在迷宫的终点处设有一个传送门，玩家通过传送门回到迷宫的起点，玩家可以选择继续探索迷宫，也可以选择从迷宫入口退出迷宫。作为探索迷宫的奖励，在这个迷宫中除了迷宫起点 (1,1)(1,1) ，每个格子都存在 11 金币，但某些格子存在守护金币的怪物，若玩家被怪物打败，玩家会被强制结束探索，接着被送进医院并且会支付 10910^9 金币的医疗费。请注意，玩家通过传送门多次探索迷宫，每个格子的金币也只能获取一次。

现在 TokitsukazeTokitsukaze 正在迷宫的起点准备探索迷宫。她会拿走她经过的所有格子上的金币（如果金币存在）。但是她目前的战斗力打不过迷宫中的任何怪物，因此她不会进入存在怪物的格子。为了使探索收益最大化，她会多次探索迷宫，在不被怪物打死的情况下，获取尽可能多的收集金币。

TokitsukazeTokitsukaze 注意到她只能在迷宫的起点处离开迷宫，一旦探索开始离开迷宫起点，直到下一次回到迷宫的起点处之前都不能离开迷宫。

根据游戏机制，迷宫会有 kk 次变化。最开始迷宫中没有怪物，第 iii 次变化将会改变格子 (xi,yi)(x_i,y_i) 的怪物状态。即若 (xi,yi)(x_i,y_i) 中没有怪物，则怪物会出现，否则怪物会消失。保证起点和终点不会出现怪物。

TokitsukazeTokitsukaze 将会在第 kk 次变化之后进入迷宫，她想知道她能获得的金币数量最大是多少。

输入描述

第一行包含一个正整数 T(1≤T≤5⋅105)T (1≤T≤5⋅10^5)，表示测试数据的组数。

对于每组测试数据：

第一行包含两个正整数 n,k(1≤n,k≤5⋅105)n, k (1≤n,k≤5⋅10^5)，表示迷宫的大小是 n×3n×3，变化的次数为 kk 次。

接下来 kk 行，每行两个正整数 xi,yi(1≤xi≤n;1≤yi≤3)x_i, y_i (1≤x_i≤n; 1≤y_i≤3)，若 (xi,yi)(x_i,y_i) 中没有怪物，则怪物出现，否则怪物消失。保证没有 (xi,yi)(x_i,y_i) 与 (1,1)(1,1) 或者 (n,3)(n,3) 相同。

保证 ∑n∑n 和 ∑k∑k 都不超过 5⋅1055⋅10^5。

输出描述

对于每组数据，输出一个整数，表示 TokitsukazeTokitsukaze 在第 kk 次变化之后进入迷宫，能获得的金币最大数量。

示例

输入：
1
5 5
3 2
4 2
5 1
4 3
4 2

输出：
6

说明

样例 11 解释：

在第一次变化后，(3,2)(3,2) 出现了怪物，TokitsukazeTokitsukaze 可以最少通过 44 次探索来获取最多的金币(路线不唯一，仅供参考)：

• 第一次走红色路线，分别获取在 (1,2)(1,3)(2,3)(3,3)(4,3)(5,3)(1,2)(1,3)(2,3)(3,3)(4,3)(5,3)格子中的总共 66 个金币。
• 第二次走绿色路线，分别获取在 (2,1)(2,2)(2,1)(2,2) 格子中的总共 22 个金币。
• 第三次走蓝色路线，分别获取在 (3,1)(4,1)(4,2)(3,1)(4,1)(4,2) 格子中的总共 33 个金币。
• 第四次走橙色路线，分别获取在 (5,1)(5,2)(5,1)(5,2) 格子中的总共 22 个金币。

当然，TokitsukazeTokitsukaze 可以继续探索迷宫，不过无法获取更多的金币。所以 TokitsukazeTokitsukaze 总共获取了 6+2+3+2=136+2+3+2=13 个金币。下图中灰色格子代表该格子的金币已经被拿走。

image-20230119212346250

同理，在第二次变化后，(4,2)(4,2)出现了怪物，TokitsukazeTokitsukaze 最多可以获取 1212 个金币，路线如下图所示。

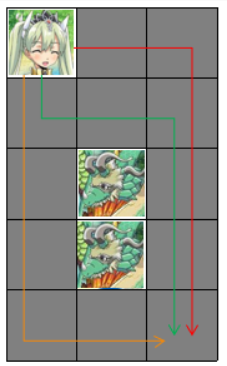
image-20230119212500177

在第三次变化后，(5,1)(5,1) 出现了怪物，TokitsukazeTokitsukaze 最多可以获取 88 个金币，路线如下图所示。

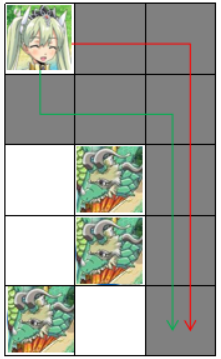
image-20230119212530328

在第四次变化后，(4,3)(4,3) 出现了怪物，若 TokitsukazeTokitsukaze 出发探索迷宫，她必定会被怪物打败，并且被送进医院然后付出高额的医疗费，所以直接退出迷宫的收益最大，因此答案是 00。

image-20230119212610318

在第五次变化后，在 (4,2)(4,2) 的怪物消失了，TokitsukazeTokitsukaze 最多可以获取 66 个金币，路线如下图所示。

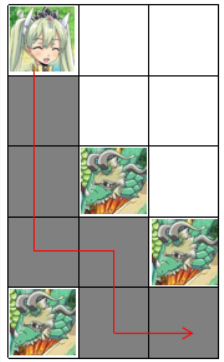
image-20230119214414023

由于这是 easy 版本，只需要输出在第五次变化后的答案即可。

示例2

输入：
3
3 4
2 2
1 3
1 3
2 2
1 2
1 2
1 2
3 2
2 3
3 2

输出：
8
2
0

分析

显然，走进怪物格子一定不是最优解，所以我们把有怪物的格子当成障碍物来看。所以题目转化为：求(1,1)(1,1)到(n,3)(n,3) 的所有路径能覆盖的格子数量。

我们可以通过两次 DFS/BFSDFS/BFS 来搜索答案：

1、从起点 (1,1)(1,1) 开始，向下/右走，标记所有能到达的格子。

2、从终点 (n,3)(n,3) 开始，向上/左走，标记所有能到达的格子。

注意本题数据较大，有一些需要注意的地方见代码，否则容易 TLETLE。

AC代码

dfs版本

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;
const int N = 5e5 + 10;
int g[N][4];
int d1[N][4], d2[N][4];
int n, k;
int dx1[] = {1, 0}, dy1[] = {0, 1};
int dx2[] = {-1, 0}, dy2[] = {0, -1};
int ans;

void dfs1(int x, int y){
	d1[x][y] = 1;
	for(int i = 0; i < 2; i++){
		int a = x + dx1[i], b = y + dy1[i];
		if(!a || a > n || !b || b > 3 || g[a][b] || d1[a][b]) continue;
		dfs1(a, b); 
	}
}

void dfs2(int x, int y){
	d2[x][y] = 1;
	for(int i = 0; i < 2; i++){
		int a = x + dx2[i], b = y + dy2[i];
		if(!a || a > n || !b || b > 3 || g[a][b] || d2[a][b]) continue;
		dfs2(a, b); 
	}
}

int main(){
	int T;
	scanf("%d", &T);
	while(T -- ){
        //数据量太大，不能memset，否则会TLE
//		memset(g, 0, sizeof g);
//		memset(d1, 0, sizeof d1);
//		memset(d2, 0, sizeof d2);
		for(int i = 1; i <= n; i++){
			for(int j = 1; j <= 3; j++){
				d1[i][j] = d2[i][j] = g[i][j] = 0; 
			}
		}
		scanf("%d%d", &n, &k);
		while(k -- ){
			int x, y;
			scanf("%d%d", &x, &y);
			g[x][y] = 1 - g[x][y];
		}
		dfs1(1, 1);
		dfs2(n, 3);

		ans = 0;
		for(int i = 1; i <= n; i++){
			for(int j = 1; j <= 3; j++){
				if(d1[i][j] && d2[i][j] && i + j != 2) ans++;
			}
		}
		printf("%d\n", ans);
	}
	
	return 0;
}

bfs版本

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;
const int N = 5e5 + 10;
int g[N][4];
int d1[N][4], d2[N][4];
int n, k;
int dx1[] = {1, 0}, dy1[] = {0, 1};
int dx2[] = {-1, 0}, dy2[] = {0, -1};
int ans;
PII q[N * 3];
int hh, tt;

void bfs(){
	hh = 0, tt = -1;
	q[++tt] = {1, 1};
	d1[1][1] = 1;
	while(hh <= tt){
		auto t = q[hh++];
		int x = t.first, y = t.second;
		for(int i = 0; i < 2; i++){
			int a = x + dx1[i], b = y + dy1[i];
			if(a > n || b > 3 || g[a][b] || d1[a][b]) continue;
			d1[a][b] = 1;
			q[++tt] = {a, b};
		}
	}
	hh = 0, tt = -1;
	q[++tt] = {n, 3};
	d2[n][3] = 1;
	while(hh <= tt){
		auto t = q[hh++];
		int x = t.first, y = t.second;
		for(int i = 0; i < 2; i++){
			int a = x + dx2[i], b= y + dy2[i];
			if(a <= 0 || b <= 0 || g[a][b] || d2[a][b]) continue;
			d2[a][b] = 1;
			q[++tt] = {a, b};
		}
	}
}

int main(){
	int T;
	scanf("%d", &T);
	while(T -- ){
        //数据量太大，不能memset，否则会TLE
//		memset(g, 0, sizeof g);
//		memset(d1, 0, sizeof d1);
//		memset(d2, 0, sizeof d2);
		for(int i = 1; i <= n; i++){
			for(int j = 1; j <= 3; j++){
				d1[i][j] = d2[i][j] = g[i][j] = 0; 
			}
		}
		scanf("%d%d", &n, &k);
		while(k -- ){
			int x, y;
			scanf("%d%d", &x, &y);
			g[x][y] = 1 - g[x][y];
		}
        
		bfs();

		ans = 0;
		for(int i = 1; i <= n; i++){
			for(int j = 1; j <= 3; j++){
				if(d1[i][j] && d2[i][j] && i + j != 2) ans++;
			}
		}
		printf("%d\n", ans);
	}
	
	return 0;
}

6、H题 《Tokitsukaze and K-Sequence》

题目描述：

TokitsukazeTokitsukaze 有一个长度为 nn 的序列 aa，她想把这个序列划分成 kk 个非空子序列。定义序列的值为这个序列中只出现一次的数字的个数。

对于 k=1…nk=1…n，TokitsukazeTokitsukaze 想知道把序列 aa 划分成 kk 个非空子序列后，所有子序列的值的和最大是多少。

请注意，子序列不一定是连续的。

输入描述：

第一行包含一个正整数 T(1≤T≤10)T (1≤T≤10)，表示测试数据的组数。

对于每组测试数据：

第一行包含一个整数 n(1≤n≤105)n (1≤n≤10^5)。

第二行包含 nn 个整数 a1,a2,…,an(1≤ai≤105)a1_,a_2,…,a_n (1≤a_i≤10^5)。

输出描述：

对于每组数据，输出 nn 个整数，第 i(1≤i≤n)i (1 ≤ i ≤ n) 个整数表示 k=ik=i 时的答案。

示例1

输入:
1
3
2 2 1

输出：
1
3
3

说明

样例11解释：

当 k=1k=1 时，aa 只能划分成 [a1,a2,a3][a_1,a_2,a_3]，即 [2,2,1][2,2,1]。其中只有 11 个数字只出现了一次，所以答案是 11。

当 k=2k=2 时，aa 可以划分成 [a1,a3][a_1,a_3], [a2][a_2]，即 [2,1][2,1] 和 [2][2]。[2,1][2,1]中有 22 个数字只出现了一次，[2][2]中有 11 个数字只出现了一次，所以答案是 2+1=32+1=3。

当 k=3k=3 时，aa 只能划分成 [a1][a_1], [a2][a_2], [a3][a_3]，即 [2][2], [2][2], [1][1]。所以答案是 1+1+1=31+1+1 = 3。

示例2

输入:
2
10
1 2 3 4 2 3 2 4 2 1
1
5

输出：
0
7
8
10
10
10
10
10
10
10
1

分析

本题属于经典思维题：单独考虑算贡献（这类思维太秀了，建议反复鞭打自己看熟！！）

赛时看了一眼以为是dpdp，没做出来。。。

可以发现每种数字的贡献可以分开计算。我们按照每种数字出现的次数进行讨论。假设数字 xx 出现的次数为cntxcnt_x

  • 如果 cntx≤kcnt_x ≤ k，我们可以贪心地将每个 xx 都分到某个子序列中，使得每个子序列要么只包含 11 个 ，要么不包含xx。所以此时数字 xx 的贡献为 cntxcnt_x。
  • 如果 cntx>kcnt_x > k，我们按照上面的方法分配完 kk 个 xx，多出来的 xx 必须分配到某个子序列中，导致那个子序列中，数字 xx 没有贡献。所以此时数字 xx 的贡献为 k−1k-1。

答案就是每种数字的贡献求和。

现在题目求 k=1...nk = 1...n 的答案。如果直接暴力统计 nn 次，会 TLETLE， 那么如何做呢？

其实可以发现对于每个 xx 的 cntxcnt_x 我们只要找到其 <=k<= k 的分界点就可以了

我们对 cntcnt 从小到大排序，枚举 k=1...nk = 1...n，答案为 cntx≤kcnt_x ≤ k 的 cntxcnt_x 求和，加上 cntx>kcnt_x > k 的 $cnt_x 的个数乘上的个数乘上(k - 1)$。
时间复杂度 O(nlogn)O(n log n)

具体实现，我们可以用multiset维护所有大于当前 kk 的 cntxcnt_x（multiset 会从小到大排序），随着 kk 的变大，某些容器头部的 cntxcnt_x 会变成小于等于 kk, 此时它们的贡献就会发生变化，即从 k−1k - 1 变成 cntxcnt_x，这个部分用一个变量累加来维护，另一部分则是当前multiset容器中的数量乘上当前的 k−1k - 1，同时这个 xx 对应的 cntxcnt_x 应当从multiset中移除（因为multiset维护的是大于 kk 的 cntxcnt_x），两者之和就是当前 kk 对应的最大的贡献和。

AC代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 100010;

multiset<int> ms; 
int n;
int a[N], cnt[N];

int main(){
	int T;
	scanf("%d", &T);
	while(T -- ){
		ms.clear();
		memset(cnt, 0, sizeof cnt);
		scanf("%d", &n);
		for(int i = 1; i <= n; i++){
			scanf("%d", &a[i]);
			cnt[a[i]]++;
		}	
		for(int i = 1; i <= N - 1; i++) ms.insert(cnt[i]);
		
		LL lesum = 0, ge = ms.size(); 
		for(int k = 1; k <= n; k++){
			while(!ms.empty() && *ms.begin() <= k){
				lesum += *ms.begin();
				ms.erase(ms.begin());
				ge--;
			}
			printf("%lld\n", lesum + ge * (k - 1));
		}
	}
	
	return 0;
}

7、J题 《Tokitsukaze and Sum of MxAb》

题目描述

TokitsukazeTokitsukaze 最近对最大值与绝对值有了兴趣。

她有一个长度为 nn 的序列 aa。

定义

MxAb(i,j)=max(∣ai−aj∣,∣ai+aj∣)MxAb(i,j)=max(∣ai−aj∣,∣ai+aj∣)

TokitsukazeTokitsukaze 想知道对于所有的 i,j(1≤i,j≤n)i, j (1≤i,j≤n)，MxAb(i,j)MxAb(i,j) 的和为多少。

即求下列式子

∑i=1n∑j=1nMxAb(i,j)\sum_{i=1}^{n} \sum_{j=1}^{n} M x A b(i, j)

输入描述

第一行包含一个整数 T(1≤T≤10)T (1≤T≤10)，表示 TT 组测试数据。

对于每组测试数据：

第一行包含一个整数 n(1≤n≤105)n (1≤n≤10^5)。

第二行包含 nn 个整数 a1,a2,…,an(−105≤ai≤105)a_1, a_2,…, a_n (−10^5 ≤ a_i ≤ 10^5)。

输出描述

对于每组测试数据，输出一个整数表示答案。

示例1

输入：
2
1
1
2
1 -2

输出：
2
12

说明

样例1解释：

第一组测试数据：MxAb(1,1)=max(∣1−1∣,∣1+1∣)=2MxAb(1,1)=max(∣1−1∣,∣1+1∣)=2

第二组测试数据：

MxAb(1,1)=max(∣1−1∣,∣1+1∣)=2MxAb(1,1)=max(∣1−1∣,∣1+1∣)=2

MxAb(1,2)=max(∣1−(−2)∣,∣1+(−2)∣)=3MxAb(1,2)=max(∣1−(−2)∣,∣1+(−2)∣)=3

MxAb(2,1)=max(∣(−2)−1∣,∣(−2)+1∣)=3MxAb(2,1)=max(∣(−2)−1∣,∣(−2)+1∣)=3

MxAb(2,2)=max(∣(−2)−(−2)∣,∣(−2)+(−2)∣)=4MxAb(2,2)=max(∣(−2)−(−2)∣,∣(−2)+(−2)∣)=4

所以总和为 2+3+3+4=122+3+3+4=12

分析

看到带有绝对值的式子，一般先展开绝对值。我们对 aia_i 和 aja_j 的正负进行讨论：

  • ai<0,aj<0 时,max⁡(∣ai−aj∣,∣ai+aj∣)=∣ai+aj∣=∣ai∣+∣aj∣a_{i}<0, a_{j}<0 \text { 时,} \max \left(\left|a_{i}-a_{j}\right|,\left|a_{i}+a_{j}\right|\right)=\left|a_{i}+a_{j}\right|=\left|a_{i}\right|+\left|a_{j}\right|

  • ai<0,aj>0 时, max⁡(∣ai−aj∣,∣ai+aj∣)=∣ai−aj∣=∣ai∣+∣aj∣a_{i}<0, a_{j}>0 \text { 时, } \max \left(\left|a_{i}-a_{j}\right|,\left|a_{i}+a_{j}\right|\right)=\left|a_{i}-a_{j}\right|=\left|a_{i}\right|+\left|a_{j}\right|

  • ai>0,aj<0 时, max⁡(∣ai−aj∣,∣ai+aj∣)=∣ai−aj∣=∣ai∣+∣aj∣a_{i}>0, a_{j}<0 \text { 时, } \max \left(\left|a_{i}-a_{j}\right|,\left|a_{i}+a_{j}\right|\right)=\left|a_{i}-a_{j}\right|=\left|a_{i}\right|+\left|a_{j}\right|

  • ai>0,aj>0 时, max⁡(∣ai−aj∣,∣ai+aj∣)=∣ai+aj∣=∣ai∣+∣aj∣a_{i}>0, a_{j}>0 \text { 时, } \max \left(\left|a_{i}-a_{j}\right|,\left|a_{i}+a_{j}\right|\right)=\left|a_{i}+a_{j}\right|=\left|a_{i}\right|+\left|a_{j}\right|

原式相当于两重循环统计，因此每个数都会被计算 2∗n2 * n 次。

AC代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
int n;
LL ans;

int main(){
	int T;
	scanf("%d", &T);
	while(T -- ){
		scanf("%d", &n);
		ans = 0;
		for(int i = 1; i <= n; i++){
			int x;
			scanf("%d", &x);
			ans += 2LL * n * abs(x);
		}
		printf("%lld\n", ans);
	}
	
	return 0;
}

8、L题 《Tokitsukaze and Three Integers》

题目描述

TokitsukazeTokitsukaze 有一个长度为 nn 的序列 aa 和一个正整数 pp 。

对于所有 x=0…p−1x=0…p−1，TokitsukazeTokitsukaze 想知道三元组 [i,j,k][i,j,k] 的数量，满足：

  • i≠j and i≠k and j≠ki \ne j \ and \ i≠k \ and \ j \ne k
  • (ai⋅aj+ak)≡x(mod p)(a_i ⋅ a_j + a_k) ≡ x (mod \ p)

输入描述

第一行包含两个整数 n,p(3≤n≤5000;1≤p≤5000)n, p (3≤n≤5000; 1≤p≤5000)。

第二行包含 nn 个整数 a1,a2,…,an(0≤ai≤109)a_1,a_2,…,a_n (0 \leq a_i \leq 10^9)。

输出描述

输出一行 pp 个整数，第 dd 个整数表示 x=dx=d 时的答案 (0≤d≤p−1)(0≤d≤p−1)。

示例

输入：
3 3
1 2 3

输出：
0 2 4

说明

样例 11 解释：

当 x=0x=0 时，没有满足条件的三元组；

当 x=1x=1 时，满足条件的三元组为；[2,3,1],[3,2,1][2,3,1] ,[3,2,1]；

当 x=2x=2 时，满足条件的三元组为；[1,2,3],[2,1,3],[1,3,2],[3,1,2][1,2,3],[2,1,3],[1,3,2],[3,1,2]。

示例2

输入：
5 10
1 2 4 5 8

输出：
6 8 8 8 6 0 6 8 4 6

分析

本题暴力计算需要 n3n^3 枚举然后统计会超时，那么如何降低到 n2n ^ 2呢，可以用预处理。

用容斥思想来做：
cxc_x 表示 ai∗aj≡x(mod p)(i≠j)a_i * a_j ≡ x (mod \ p)(i≠j) 的个数，可以在 O(n2)O(n^2) 的时间复杂度内计算出来。接下来枚举 kk ,计算 ansans。满足 (ai∗aj)+ak≡x(mod p)(i≠j)(a_i * a_j) + a_k ≡ x (mod \ p)(i≠j)，时间复杂度为 O(np)O(np)。
但这样会把 i=ki=k 或者 j=kj=k 的情况计算进答案，我们需要把这部分减掉。枚举 i=ki= k 的情况，减去 ansxans_x。满足(ai∗aj)＋ai≡x(modp)(i≠j)(ai * aj)＋ a_i ≡ x (mod p)(i≠j)，j=kj= k 的情况同理。时间复杂度为 O(n2)O(n^2)。
总时间复杂度为O(n2+np)O(n^2+ np)。

因此一共预处理两个数组：

c[N]:c[N]: 其中 c[v]c[v] 代表 a[i] * a[j] % p = v 的 (i,j)(i, j) 数对的数量。

d[N][N]:d[N][N]: 其中 d[k][v]d[k][v] 代表两项乘积中其中一项等于第 kk 项并且 a[i] * a[j] % p = v 的数量。

AC代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 5010;
int c[N], d[N][N];
int a[N];
int n, p; 

int main(){
	scanf("%d%d", &n, &p);
	for(int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
		a[i] %= p;
	}
	//预处理 
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n; j++){
			if(i == j) continue;
			c[a[i] * a[j] % p]++;
			d[i][a[i] * a[j] % p] += 2;
		}
	}
	
	for(int x = 0; x <= p - 1; x++){
		LL ans = 0;
		for(int k = 1; k <= n; k++){
			int v = (x - a[k] + p) % p; 
			ans += c[v] - d[k][v];
		}
		printf("%lld ", ans);
	}
	puts("");	
    
	return 0;
}

未完待续。。。(别问我为什么又是未完)

上一篇： 牛客寒假集训营第三场补题