牛客寒假集训营第三场补题

yuanheci 2023年01月24日 184次浏览

纯纯的数学场~

1、B题《勉强拼凑的记忆》

题目描述

小红希望用恰好 $n$ 块矩形积木来搭建正方形，其中小红可以自由选择每块积木的大小，但必须是 $1∗k$ 的长和宽。其中 $1\leq k \leq \lceil \frac{n}{2} \rceil$ 。小红想知道，自己最大可以搭建多大的正方形？请你帮小红计算正方形的边长。如果无法用恰好 $n$ 块矩形拼成正方形，请输出 $-1$ 。

输入描述

第一行输入一个正整数 $t$ ，代表询问的次数。
接下来的 $t$ 行，每行输入一个正整数 $n$ ，代表一次查询。
$1≤t≤200000$
$1≤n≤10^{18}$

输出描述

输出 $t$ 行，每行输入一个正整数，代表可以拼成的正方形最大边长。

示例1

输入：
3
2
4
6

输出：
-1
2
4

说明

$n=2$ 时，只能使用 $1*1$ 的积木，显然恰好两个积木无法拼成任何正方形。

$n=4$ 时， $2*2$ 正方形的拼法（ $4$ 个 $1*1$ 即可）：

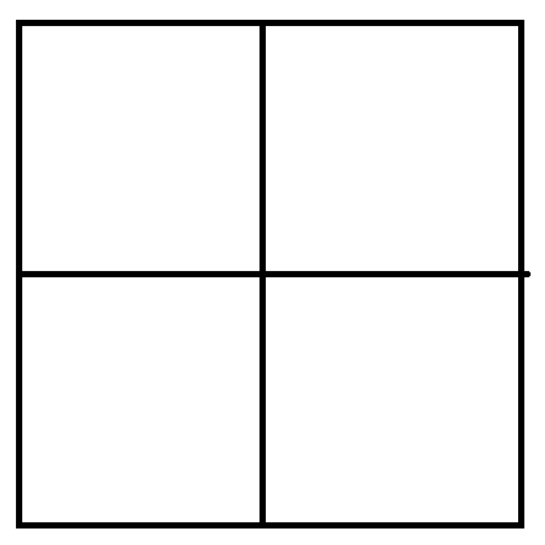
$n=6$ 时， $4*4$ 正方形的拼法：

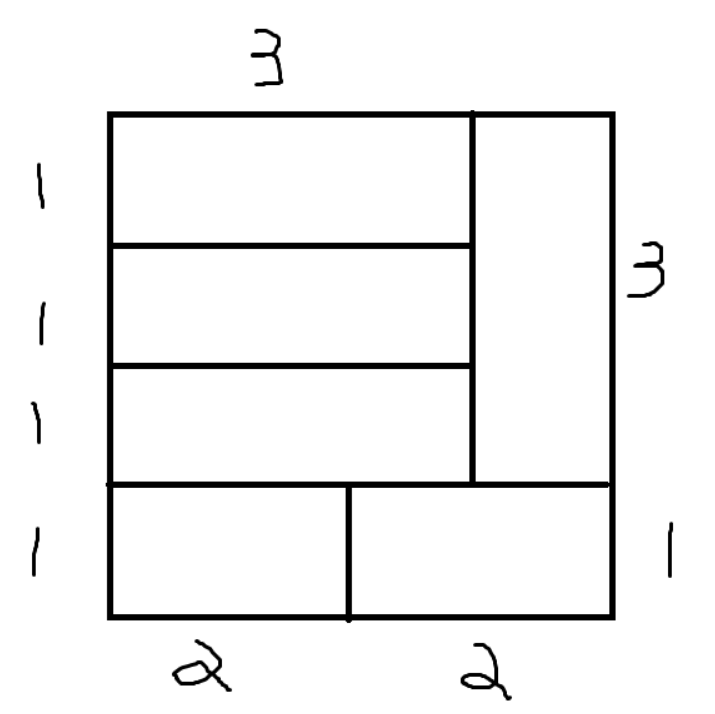
分析

sss

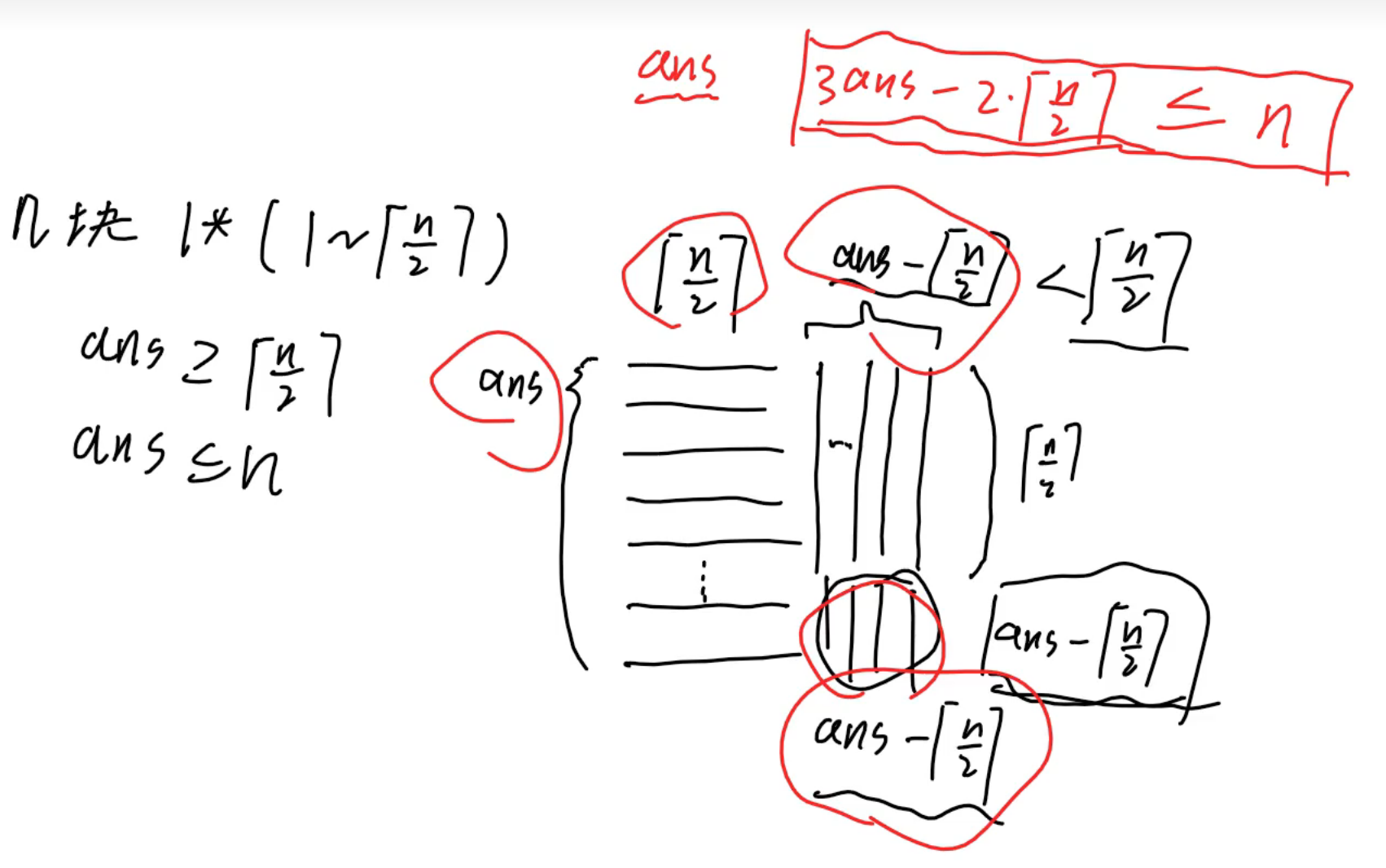
为什么这样是面积最大的？

因为我们尽可能多地使用了 $1 * \lceil \frac{n}{2} \rceil$ 的长方形；

最终得到的是边长为 $ans$ 的正方形。

AC代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
LL n; 

int main(){
	int T;
	scanf("%d", &T);
	while(T -- ){
		scanf("%lld", &n);
		if(n == 2) puts("-1");
		else{
			LL v = n + 2 * ((n + 2 - 1) / 2);
			printf("%lld\n", v / 3);
		}
	}
	
	return 0;
}

2、C题《忽远忽近的距离》

题目描述

小红希望你构造一个长度为 $n$ 的排列，满足对于每个 $a_i$ ，有 $2\le |a_i-i|\le 3$ 。你能帮帮她吗？

注：数组下标从 $1$ 到 $n$ 。

排列是指长度为 $n$ 的数组， $1$ 到 $n$ 每个正整数恰好出现一次。

输入描述

一个正整数 $n$
$1≤n≤10^5$

输出描述

如果无解，请输出 $-1$ 。
否则输出任意合法解即可。

示例1

输入:
4

输出：
3 4 1 2

分析

本题为构造题目，这类题做得比较少。。。

可以发现， $n = 4$ 时， $3, 4, 1, 2$ 是可行的方案； $n = 5$ 时， $3, 4, 5, 1, 2$ 是可行的方案； $n = 6$ 时， $4, 5, 6, 1, 2, 3$ 是可行的方案，而 $n = 7$ 时不可行， $n$ 取到更大时，都可行，通过 $n - 4$ 的方案再加上一个 $4$ 的情况即可构造出一种方案。

因此本题无解的特殊情况是 $n <= 3 \ OR \ n == 7$

对于一个数 $n$ ，可以通过 $dfs$ 来搜索一种可行的方法，即用 $4, 5, 6$ 来拼凑出 $n$ 。

AC代码

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;
int n; 
int a[] = {4, 5, 6};
vector<int> path;

bool dfs(int u, int sum){
	if(sum > n) return false;
	if(sum == n) return true;
	for(int i = 0; i < 3; i++){
		path.push_back(a[i]);
		if(dfs(i, sum + a[i])) return true;
		path.pop_back();
	}
	return false;
}

int main(){
	scanf("%d", &n);
	if(n <= 3 || n == 7) puts("-1");
	else{
		dfs(0, 0);
		int idx = 1;
		for(auto& s : path){
			if(s == 4){
				printf("%d %d %d %d ", idx + 2, idx + 3, idx, idx + 1);
				idx += 4;
			}
			else if(s == 5){
				printf("%d %d %d %d %d ", idx + 2, idx + 3, idx + 4, idx, idx + 1);
				idx += 5;
			}
			else if(s == 6){
				printf("%d %d %d %d %d %d ", idx + 3, idx + 4, idx + 5, idx, idx + 1, idx + 2);
				idx += 6;
			}
		}			
	}
	
	return 0;
}

3、E题《公平守望的灯塔》

题目描述

小红在平面直角坐标系上选择了两个点 $A$ 和 $B$ （保证两点不重合），它们的坐标分别为 $(x_A,y_A)$ 和 $(x_B,y_B)$ 。小红希望你选择一个整点 $C$ ，满足三角形 $ABC$ 为 $AB$ 为斜边的等腰直角三角形。你能帮帮她吗？
整点的定义：横坐标和纵坐标均为整数。

输入描述

四个整数 $x_A,y_A,x_B,y_B$ ，用空格隔开。
$−10^9≤x_A,y_A,x_B,y_B≤10^9$

输出描述

如果无解，请直接输出 “No Answer!”
否则输出两个整数 $x_C,y_C$ ，代表 $C$ 点的坐标。有多解时输出任意即可。

示例

输入：
1 0 0 1

输出：
0 0

说明：
输出1 1也是可以的。

分析

本题最简单的方法是用向量来计算，学到了学到了~。比赛中用了联立方程组来求解，过程比较复杂而且最终应该是由于精度问题只过了 $70$ % 的数据。

$(x, y)$ 向量旋转 $90°$ 后为 $(x, -y)$ 或者 $(-x, y)$ ；因为两个向量垂直等价于两个向量点积为 $0$ 。

设 $A(x_A, y_A)$ ， $B(x_B, y_B)$ ，则 $\overrightarrow {AB} = (x_B - x_A, y_B - y_A)$ 。

据此就可以计算了。

AC代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
LL xa, xb, ya, yb;

int main(){
	scanf("%lld%lld%lld%lld", &xa, &ya, &xb, &yb);
	LL x = xa + xb - yb + ya, y = ya + yb - xa + xb;
	if((x % 2 != 0) || (y % 2 != 0)) puts("No Answer!");
	else printf("%lld %lld", x / 2, y / 2);
	
	return 0;
}

4、G题《严肃古板的秩序》

题目描述

小红拿到了一个运算式，其中有一些地方可以填入’+‘、’-‘、’#‘（不允许添加括号）。问最终是否可以使得等式成立。若可以，输出任意合法解。否则输出 $-1$ 。
其中’+‘和’-‘代表四则运算的加法或者减法，’#‘符号是小红发明的新运算符号： $a$ # $b$ 为 $a$ 的 $a$ 次方对 $b$ 取模。例如 $3$ # $5=3^3 mod \ 5=2$ 。’#'符号的运算优先级和加减法是相同的（从左到右进行运算）。
在本题中，我们定义 a#b 当且仅当 $a$ 和 $b$ 都是正整数时是有意义的。

输入描述

一个字符串，该字符串仅包含阿拉伯数字和问号、等号的字符串。保证字符串满足以下性质：
$1$ 、字符串仅由阿拉伯数字、'?‘和’=‘组成，第一个字符保证是阿拉伯数字，不存在两个相邻的’?‘字符。
2、保证有且仅有一个’=‘字符，’=‘字符保证不是字符串最后一个字符，’=‘的左边相邻和右边相邻的一定是阿拉伯数字且’=‘右边所有字符均为阿拉伯数字。
$3$ 、所有阿拉伯数字表示的数均为不超过 $10^9$ 的非负整数，若该数为正整数，则保证不包含前导零。
$4$ 、’?'的数量不超过 $12$ 个。

输出描述

如果存在合法解，请输出一个字符串，代表最终的运算式。否则输出 $-1$ 。

请务必保证，你输出的字符串将所有的’?‘修改成了’+‘、’-‘或者’#'，且未修改阿拉伯数字和等号。不得添加或删除新字符。

示例1

输入：
2?1?2?2=3

输出：
2-1#2+2=3

说明：
该答案并不是唯一的。

示例2

输入：
5?2=2

输出：
-1

示例3

输入：
5?8=13

输出：
5+8=13

分析

本题为纯码力题，暴力搜索完所有情况即可。

需要注意的两点：

1、算出 $0$ 或者负数时若下一步是’#'运算，则应该直接终止。

2、当底数为 $long \ long$ 类型时，快速幂应将底数取模，指数不用取模，底数可能因为 $a * a$ 爆 $long \ long$ 。

AC代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 4;
string s; 
vector<int> nums;
vector<char> op; 
bool st[N];
char str[] = {'+', '-', '#'}; 
int cnt;
int res;

int qmi(LL a, LL k, int mod){
	int ans = 1;
	a %= mod;   //要对底数取模，否则可能爆LL 
	while(k){
		if(k & 1) ans = 1LL* ans * a % mod;
		a = 1LL* a * a % mod;
		k >>= 1; 
	}
	return ans;
}

bool dfs(int u){
	if(u >= cnt){
		int idx1 = 0, idx2 = 0; //idx1操作nums，idx2操作op 
		LL l = nums[idx1++];
		LL cur;
		for(auto& oc : op){
			int r = nums[idx1++];
			if(oc == '#' && (l <= 0 || r <= 0)) return false;
			if(oc == '+') cur = l + r;
			else if(oc == '-') cur = l - r;
			else if(oc == '#') cur = qmi(l, l, r);
			l = cur;
		} 
		if(l == res) return true;
		else return false;
	}
	for(int i = 0; i < 3; i++){
		op.push_back(str[i]);
		if(dfs(u + 1)) return true;
		op.pop_back();
	}
	return false;
}

int main(){
	cin >> s;
	string x = "";
	for(int i = 0; i < s.size(); i++){
		if(s[i] >= '0' && s[i] <= '9') x += s[i];
		else{	
			if(s[i] == '?') cnt++;		 
			nums.push_back(atoi(x.c_str()));
			x = "";
		}
	}
	res = atoi(x.c_str());

	//开始dfs
	if(dfs(0)){
		int idx = 0;
		for(auto& c : s){
			if(c != '?') printf("%c", c);
			else printf("%c", op[idx++]);
		}
	}
	else puts("-1");
	
	return 0;
}

上一篇：牛客寒假集训营第四场补题下一篇：牛客寒假集训营第二场补题