数论分块

===========>学习博客传送门

====>题目整理

分块是一种思想，而不是一种数据结构

之前接触到的莫队算法中也用到了分块的思想。====>莫队算法传送门

数论整除分块可以在 $O(\sqrt{n})$ 的时间复杂度内计算以下式子：${\large \sum_{1}^{n}f(\left \lfloor \frac{n}{i} \right \rfloor)}$

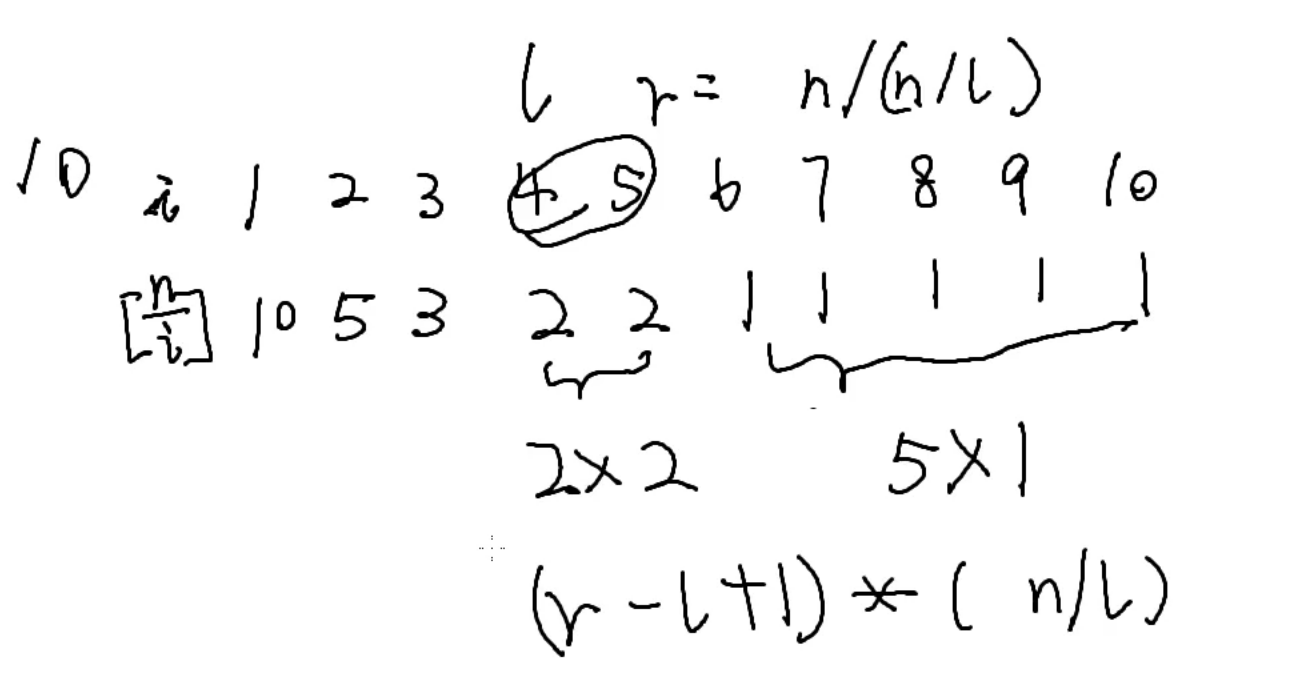
1、板子题 H(n)

板子题： https://www.luogu.com.cn/problem/UVA11526

AC代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

int t;

LL solve(LL n){
	LL res=0;
	for(LL i = 1, j = 0; i <= n; i = j + 1){
		j = n / (n / i);
		res += (j - i + 1) * (n / i);
	}
	return res;
}

signed main(){
	cin >> t;
	while(t -- ){
		LL n;
		cin >> n;
		cout << solve(n) << '\n';
	}
	return 0;
}

2、P3935 Calculating

《P3935 Calculating》

然后就可以用分块了。

#include <bits/stdc++.h>
using namespace std;
 
typedef long long LL; 
const int MOD = 998244353;
LL a, b; 
 
int calc(LL x) {
	int ans = 0;
	for(LL l = 1, r; l <= x; l = r + 1){
		r = x / (x / l);
		ans = (ans + 1LL* (r - l + 1) * (x / l) % MOD) % MOD;
	}
	return ans;
}
 
void solve(){
	scanf("%lld%lld", &a, &b);
	printf("%d\n", (calc(b) - calc(a - 1) + MOD) % MOD);
}
 
int main(){
	int T = 1;
//	scanf("%d", &T);
	while(T -- ){
		solve();
	}
}

3、P1403 [AHOI2005]约数研究

P1403 [AHOI2005]约数研究

#include <bits/stdc++.h>
using namespace std;
 
typedef long long LL; 
int n;
LL ans;
 
void solve(){
	scanf("%d", &n);
	for(int l = 1, r; l <= n; l = r + 1){
		r = n / (n / l);
		ans += 1LL* (r - l + 1) * (n / l);	
	}
	printf("%lld\n", ans);
}
 
int main(){
	int T = 1;
//	scanf("%d", &T);
	while(T -- ){
		solve();
	}
}

4、P2261 [CQOI2007]余数求和

https://www.luogu.com.cn/problem/P2261

该题运用整除分块较为灵活。

#include <bits/stdc++.h>
using namespace std;
 
typedef long long LL; 
int n, k;

LL calc(){
	LL ans = 0;
	for(int l = 1, r; l <= n; l = r + 1){
		if(k / l == 0) r = n;
		else r = min(k / (k / l), n);
		ans += 1LL* (k / l) * (l + r) * (r - l + 1) / 2; 
	}
	return ans;
}

void solve(){
	scanf("%d%d", &n, &k);
	printf("%lld\n", 1LL* n * k - calc());
}
 
int main(){
	int T = 1;
//	scanf("%d", &T);
	while(T -- ){
		solve();
	}
}

5、AtCoder abc296——D题

https://atcoder.jp/contests/abc296/tasks/abc296_d

#include <bits/stdc++.h>
using namespace std;
 
typedef long long LL; 
LL n, m;
 
void solve1(){
	scanf("%lld%lld", &n, &m);
	
	LL x = m / n;
	if(x >= n) {
		if(x > n){
			puts("-1");
			return;
		}
		if(x == n && m % n){
			puts("-1");
			return;
		}
	}
	
	LL ans = 1e18;
	for(LL l = 1, r; l <= m; l = r + 1){
		r = m / (m / l);
		LL l2 = (m + l - 1) / l;  //上取整，保证乘积大于等于m
		if(l <= n && l2 <= n) ans = min(ans, l * l2);
	}
	printf("%lld\n", ans);
}
 
int main(){
	int T = 1;
//	scanf("%d", &T);
	while(T -- ){
		solve1();
	}
}

6、Problem - 1485C - Codeforces

n/(i+1)形式的数论分块

Problem - 1485C - Codeforces

本题也可以不用数论分块，直接确定范围后枚举计算

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
int x, y;

// ---n/(i+1)形式的数论分块--有特殊性需要注意 
//根据打表n=20时
//得到结论r=n/(n/l)，应该改为r=n/(n/l)-1，因为实际上是n/(l+1)<=k,即l+1<=n/k,l<=n/k-1 

void solve(){
	scanf("%d%d", &x, &y);
	LL ans = 0;
	int i;
	for(i = 1; i <= x / i && i <= y; i++) ans += (1LL*i * i + i - 1 ) / (i + 1);
	for(int j; i <= y; i = j + 1){
		if(i + 1 > x) break;
		j = min(y, x / (x / (i + 1)) - 1);
		ans += (1LL*j - i + 1) * (x / (i + 1));
	} 
	printf("%lld\n", ans);
}

int main(){
	int _ = 1; scanf("%d", &_);
	while(_--) solve();
	return 0;
}