扫描线一般用于解决面积并的问题,最简单的应用是求矩形的面积并。
直观理解(不过一般使用的扫描线是从左到右扫描,知道是这么个过程就行):
使用针对不同数据范围可以有两种方式。
方式一: 利用区间合并暴力求解,时间复杂度为O(n^2),可以用于解决数据量为1e3级别的问题。
方式二: 利用线段树 + 扫描线,时间复杂度为O(nlogn),可以用于解决数据量为1e5级别的问题。
下面就让我们来看看扫描线的基本用法吧~
1、暴力计算O(n^2)
1.1、题目
我们给出了一个(轴对齐的)二维矩形列表 rectangles 。对于 rectangle[i] = [xi1, yi1, xi2, yi2],表示第 i 个矩形的坐标,(xi1, yi1) 是该矩形左下角的坐标,(xi2, yi2) 是该矩形右上角 的坐标。
计算平面中所有 rectangles 所覆盖的总面积 。任何被两个或多个矩形覆盖的区域应只计算一次 。
返回总面积。因为答案可能太大,返回 10^9 + 7 的 模 。
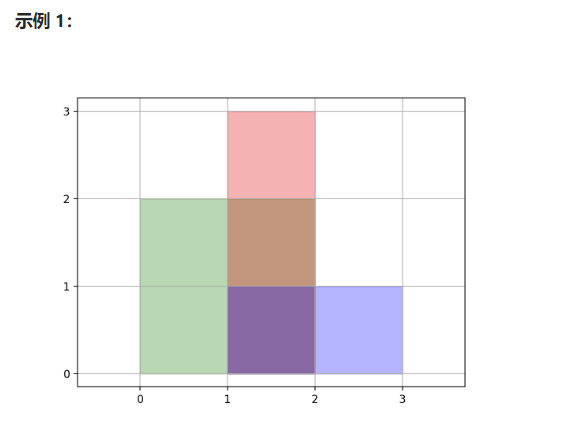
数据1
输入:rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出:6
解释:如图所示,三个矩形覆盖了总面积为6的区域。
从(1,1)到(2,2),绿色矩形和红色矩形重叠。
从(1,0)到(2,3),三个矩形都重叠。
数据2
输入:rectangles = [[0,0,1000000000,1000000000]]
输出:49
解释:答案是 1e18 对 (1e9 + 7) 取模的结果,即49 。
提示:
1 <= rectangles.length <= 200
rectanges[i].length = 4
0 <= xi1, yi1, xi2, yi2 <= 1e9
矩形叠加覆盖后的总面积不会超越2^63 - 1 ,这意味着可以用一个64位有符号整数来保存面积结果。
1.2、分析
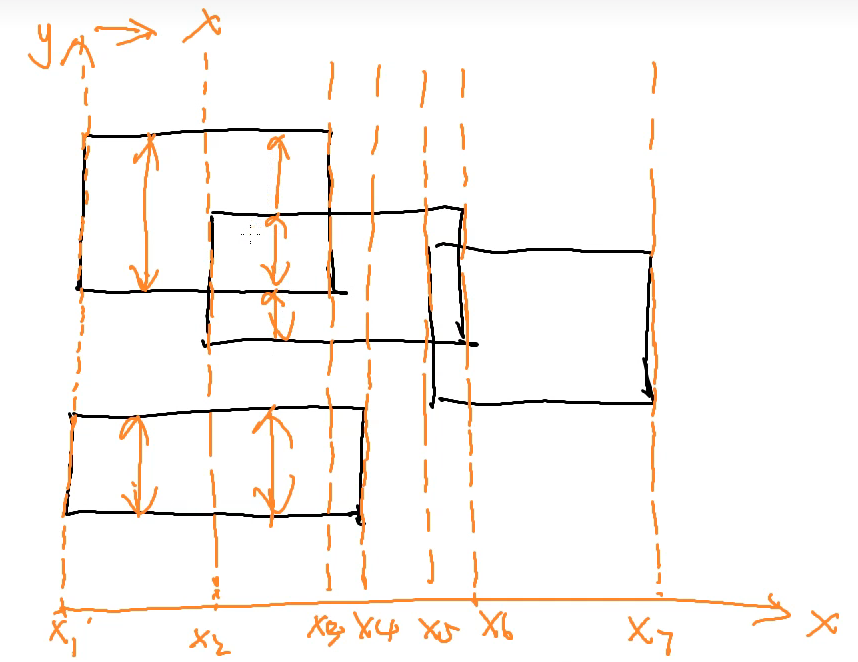
(1) 扫描线是纵向的线,从左到右扫过去。
(2) 横坐标中临界点就是每个矩形的其实列和终止列的横坐标,我们根据这些边界划分好一个个的区域,如 x1~x2 是一个区域,x2~x3 是一个区域。。。然后对于每个区域统计矩形的高度,利用积分的思想,将每一段的高度加到一起就可以了。
可以发现扫描线解决矩形的面积并思路还是比较清晰明了的,那么具体如何做呢?
(1) 首先,对于横坐标的处理:
题目中给定的是每个矩形的左下角坐标和右上角坐标,其实就是给出了每个矩形的纵向起始边(左边那条)和终止边(右边那条)的横坐标,我们将所有矩形的横坐标全部加入一个集合中来维护,然后排个序即可。
(2) 然后,是对于纵坐标的处理:
在上一步中我们处理好了横坐标,相当于是处理好了一个个的计算区间,然后我们需要计算每一个计算区间的高度的积分,可以通过一个pair数组来维护每一段高度,然后可以使用区间合并的思想。我们遍历题目给出的所有矩形的左右边界,如果满足条件x1 <= l && x2 >= r那么说明这个矩形能够在当前这个[l, r]计算区间内做高度的贡献,我们就把它加入这个计算区间的高度的集合中。遍历完所有矩形后,对高度的集合排序。然后就可以做一遍区间合并,求出高度的积分(其实就是总长啦·~)。到这里我们就可以计算面积了, s = (r - l) * len。
1.3、代码
#define x first
#define y second
typedef long long LL;
typedef pair<LL, LL> PLL;
class Solution {
public:
int mod = 1e9 + 7;
vector<int> a; //横坐标
vector<vector<int>> g;
PLL b[410]; //每个高度的区间
LL get_area(int l, int r){
int cnt = 0;
LL len = 0;
for(auto& y : g){
if(y[0] <= l && y[2] >= r) { //该矩形包含了[l, r],才可以算贡献
LL maxy = max(y[1], y[3]);
LL miny = min(y[1], y[3]);
b[cnt++] = {miny, maxy};
}
}
if(cnt == 0) return 0;
sort(b, b + cnt); //按照左端点排序,做区间合并
LL st = b[0].x, ed = b[0].y;
for(int i = 1; i < cnt; i++){
if(b[i].x <= ed) ed = max(ed, b[i].y);
else{
len += ed - st;
st = b[i].x, ed = b[i].y;
}
}
//最后一段加入
len += ed - st;
return len * (r - l);
}
int rectangleArea(vector<vector<int>>& gr) {
this->g = gr;
for(auto& x : g){
a.push_back(x[0]);
a.push_back(x[2]);
}
sort(a.begin(), a.end());
LL ans = 0;
//把每个计算区间算出来的面积加在一起
for(int i = 0; i < a.size() - 1; i++)
ans = (ans + get_area(a[i], a[i + 1])) % mod;
return ans;
}
};
2、线段树加速计算O(nlogn)
讲完了扫描线的暴力做法,接下来进入重头戏,用线段树加速计算,使得时间复杂度降低到O(nlogn)。
2.1、题目《亚特兰蒂斯》
有几个古希腊书籍中包含了对传说中的亚特兰蒂斯岛的描述。
其中一些甚至包括岛屿部分地图。
但不幸的是,这些地图描述了亚特兰蒂斯的不同区域。
您的朋友 Bill 必须知道地图的总面积。
你自告奋勇写了一个计算这个总面积的程序。
输入格式
输入包含多组测试用例。
对于每组测试用例,第一行包含整数 n,表示总的地图数量。
接下来 n 行,描绘了每张地图,每行包含四个数字 x1,y1,x2,y2(不一定是整数),(x1,y1) 和 (x2,y2) 分别是地图的左上角位置和右下角位置。
注意,坐标轴 x 轴从上向下延伸,y 轴从左向右延伸。
当输入用例 n = 0 时,表示输入终止,该用例无需处理。
输出格式
每组测试用例输出两行。
第一行输出 Test case #k,其中 k 是测试用例的编号,从 1 开始。
第二行输出 Total explored area: a,其中 a 是总地图面积(即此测试用例中所有矩形的面积并,注意如果一片区域被多个地图包含,则在计算总面积时只计算一次),精确到小数点后两位数。
在每个测试用例后输出一个空行。
数据范围
1≤n≤10000,
0≤x1<x2≤100000,
0≤y1<y2≤100000
注意,本题 n 的范围上限加强至 10000。
输入样例
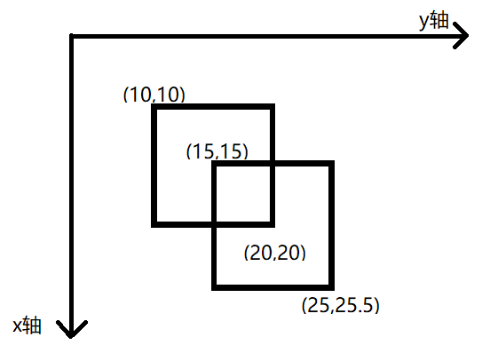
2
10 10 20 20
15 15 25 25.5
0
输出样例
Test case #1
Total explored area: 180.00
样例解释
样例所示地图覆盖区域如下图所示,两个矩形区域所覆盖的总面积,即为样例的解。
2.1、核心思想
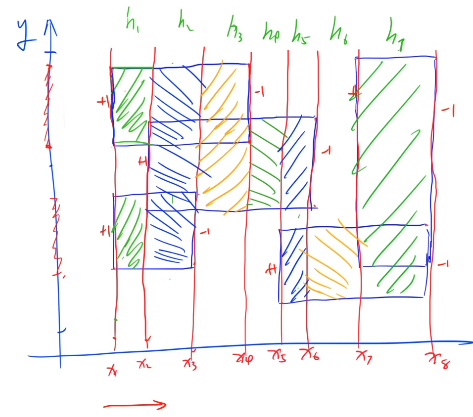
(1) 我们的线段树就是为了维护矩形的高度,因此对y轴方向建立线段树。我们 给每一个矩形的左右边进行标记,左边的边标记为 1,右边的边标记为 -1,从左往右扫描每遇到一个矩形时,我们知道了标记为 1 的边,我们就加进来这一条矩形的高,等到扫描到 -1 时,证明这一条边需要删除,就删去,利用 1 和 -1 可以轻松的到这种状态。
(2) 还要注意这里的线段树指的并不是线段的一个端点,而指的是一个区间,所以如果我们维护的区间是[l, r],那么在线段树中维护的是[l, r - 1],因为l在线段树中代表区间[l, l + 1], r - 1代表区间[r - 1, r]。
(3) 由于题目给出的坐标一般是小数,因此需要离散化。
2.2、具体分析
我们将纵向的线段按照横坐标进行排序,然后从左到右扫描,将每个横坐标上的纵向线段都加入线段树 (modify操作)。
因此我们需要的操作有:
(1) 将某个区间[l, r] + k。
(2) 求整个区间中长度大于0的区间总长是多少。
线段树中需要维护的节点信息有:
(1) cnt : 当前区间被整个覆盖的次数(大于0了不管值是多少都一样)。
(2) len : 不考虑祖先结点cnt的前提下,cnt > 0的区间总长(线段树中永远向下看)。
这里用到的线段树非常特殊,虽然我们需要实现区间修改,但是不需要pushdown操作,这样大大简化了线段树的写法难度。注意这里是专门针对求矩形面积并问题的处理方式(对于其它图形如三角形,普通平行四边形等不适用,就必须得用pushdown了),下面来讲讲为什么不需要pushdown操作。
在一般的带懒标记的线段树中,需要在modify和query操作中执行pushdown,而矩形面积并问题有一个非常重要的性质:所有操作都是成对出现的,并且固定是先加后减。 因此对于任何一个区间而言,线段树中维护的cnt都是大于等于0的,分类讨论一下:
(1) 对于modify操作而言:
① 如果cnt > 0,那么说明这个区间是要算上的,其只要cnt > 0了,那么就和cnt具体是多少无关。并且我们每次查询需要查询的是整个y方向的区间,因此pushdown修改它的子结点是无意义的操作。
② 如果cnt = 0,那么说明这个区间上没有懒标记,当然也就不用往下传喽,在pushdown中尚且还要判断if(root.lazy)来执行。
(2) 对于query操作而言:
我们每次查询的是y方向的整个区间,即查找的是线段树最顶层的那个结点tr[1],所以用不到pushdown操作。
(3) 更多具体细节详见代码。
2.3、代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10010;
struct Segment{ //存储纵向每一段的信息
double x, y1, y2;
int k;
bool operator< (const Segment& t) const{
return x < t.x;
}
}seg[N * 2];
struct Node{ //线段树
int l, r;
int cnt;
double len;
}tr[N * 8]; //每个输入最多有两个y值,所以最多有N * 2 * 4空间
vector<double> ys; //y坐标离散化
int n;
int find(double y){ //二分找到离散化后的下标,找的是第一个大于等于y的下标
int l = 0, r = ys.size() - 1;
while(l < r){
int mid = l + r >> 1;
if(ys[mid] >= y) r = mid;
else l = mid + 1;
}
return l;
}
void pushup(int u){
//高度区间长度 = 右端点-左端点
//注意线段树中维护的是区间,所以tr[u].r表示的是tr[u]中最后一小段区间的左端点
if(tr[u].cnt) tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];
//因为cnt代表的是当前区间是否被完整覆盖,因此虽然当前区间没有被完整覆盖,
//但是其中的部分几段可以被覆盖呀!所以从左右子结点中整合信息即可。
else if(tr[u].l != tr[u].r) { //不是叶子
tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}
else tr[u].len = 0; //是叶子,代表的是长度为1的最小区间,由于没有被覆盖且无法再分,所以len=0
}
void build(int u, int l, int r){
tr[u] = {l, r, 0, 0};
if(l != r){
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);//因为初始建树时cnt和len都为0,所以没必要pushup
}
}
void modify(int u, int l, int r, int k){
if(tr[u].l >= l && tr[u].r <= r) {
tr[u].cnt += k;
pushup(u); //因为 +k 可能导致cnt变成0,而len还没改变,因此需要pushup一下
}
else{
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(u << 1, l, r, k);
if(r > mid) modify(u << 1 | 1, l, r, k);
pushup(u);
}
}
int main(){
int T = 1;
while(scanf("%d", &n), n){
ys.clear();
double x1, y1, x2, y2;
for(int i = 0, j = 0; i < n; i++){
scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
seg[j++] = {x1, y1, y2, 1};
seg[j++] = {x2, y1, y2, -1};
ys.push_back(y1), ys.push_back(y2);
}
//y方向离散化
sort(ys.begin(), ys.end());
ys.erase(unique(ys.begin(), ys.end()), ys.end());
sort(seg, seg + 2 * n);
//线段树中维护的是区间,所以是ys.size() - 1 - 1
//ys.size() - 1是最后一个点,那么最后一段区间的左端点应该要再减1
build(1, 0, ys.size() - 2);
double ans = 0;
for(int i = 0; i < 2 * n; i++){
if(i > 0) ans += tr[1].len * (seg[i].x - seg[i - 1].x); //第一条纵向线前面没有东西,为0
//修改操作,修改[l, r]在线段树中就是修改[l, r - 1],线段树中l代表区间l ~ l+1, r-1代表r-1 ~ r
modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);
}
printf("Test case #%d\n", T++);
printf("Total explored area: %.2lf\n\n", ans);
}
return 0;
}
3、实际应用
https://leetcode.cn/problems/perfect-rectangle/description/
1、将每个矩形由点的表示转化为两条竖直边的表示,每个竖直边以(x, y1, y2, c)的形式进行存储,其中c=1表示是左边的竖直边,c = -1表示是右侧的竖直边。下面将这些竖直边统称为扫描线。
2、对所有扫描线按照其x值从小到大排序,x相同则按照y1的值从小到大排序。
3、对于所有x相同的扫描线,按照flag的不同分为两个集合seg_l和seg_r,分别储存当前x坐标左边的扫描线和右边的扫描线。在将新的扫描线合并到seg_l或者seg_r的过程中:
3.1 如果发生线段的重叠, 则直接返回false
3.2 如果新线段的y1值等于集合中最后一个线段的y2值,则更新集合中最后一个线段的y2
3.3 否则将该线段加入到对应的集合中
4、判断是否是完美矩形
4.1 对于非边缘的扫描线,如下图所示,需要非边缘的扫描线恰好出现在左扫描线和右扫描线各一次,即满足seg_l和seg_r的元素完全相等
4.2 对于边缘的扫描线,只能在某个集合中出现一次,并且该集合中有且只有这一条扫描线,以左边缘扫描线为例,需满足 seg_l.size() = 1 && seg_r.empty()。
class Solution {
public:
typedef pair<int, int> PII;
#define x first
#define y second
struct Seg{
int x, y1, y2, c;
bool operator< (const Seg& t) const{
if(x != t.x) return x < t.x;
else return y1 < t.y1;
}
}seg[40010];
int idx;
void merge(vector<PII>& vs, int x, bool &ok){
if(vs.empty()) vs.push_back({seg[x].y1, seg[x].y2});
else{
auto &last = vs.back();
if(seg[x].y1 < last.y) ok = false;
else if(seg[x].y1 == last.y) last.y = seg[x].y2;
else vs.push_back({seg[x].y1, seg[x].y2});
}
}
bool isRectangleCover(vector<vector<int>>& g) {
int n = g.size();
for(int i = 0; i < n; i++){
seg[idx++] = {g[i][0], g[i][1], g[i][3], 1};
seg[idx++] = {g[i][2], g[i][1], g[i][3], -1};
}
sort(seg, seg + idx);
for(int i = 0; i < idx; i++){
vector<PII> sl, sr; //统计左右边界的集合
int j = i;
//找出所有x相等的线段
while(j < idx && seg[i].x == seg[j].x) j++;
for(int k = i; k < j; k++){
bool ok = true;
if(seg[k].c == 1) merge(sl, k, ok);
else merge(sr, k, ok);
if(!ok) return false;
}
if(i > 0 && j < idx){ //内部线段
if(sl.size() != sr.size()) return false;
for(int u = 0; u < sl.size(); u++){
if(sl[u].x != sr[u].x || sl[u].y != sr[u].y) return false;
}
}
else if(i == 0){
if(!(sl.size() == 1 && sr.size() == 0)) return false;
}
else{
if(!(sr.size() == 1 && sl.size() == 0)) return false;
}
i = j - 1;
}
return true;
}
};