概率与期望在算法中的常见模型

  期望和概率还是十分重要的模块，就稍微学习并记录一下hh。

一、离散型随机变量

1、有用的知识

1.1、概率的巧妙转换

1.2、期望用概率表示

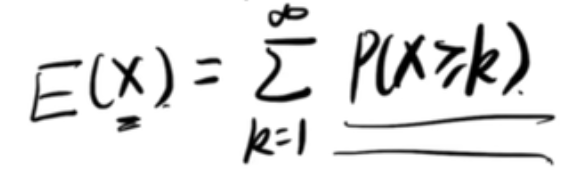
举例应用：

  注意应用场景为求次数的期望，别乱用~

2、随机游走

2.1、链式

  一条长度为 $n$ 的链，从一端走到另一端的期望时间。
  分析方式： 定义 $E(x)$ 表示 第一次从 $x$ 到达 $x + 1$ 所花费的期望时间，然后用期望DP求解即可。

  模型为： 每一步，你有 $p$ 的概率往左走一步，同时也有 $1 - p$ 的概率往右走一步 $/$ 走到某个点等。

  注意： 初值的设定要根据实际情况来设置，不一定都为 $1$，最终的结果是 $\sum{E(i)}$ 求和的值。

  之前博客中写过的一道$cf$题也是这个类型。
  《Flexible String Revisit》

  题目：
  《爬树的甲壳虫》

《爬树的甲壳虫》AC代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 100010, MOD = 998244353;
int x[N], y[N];
int f[N], s[N];
int n; 
int ans;

int qmi(int a, int k){
	int ans = 1;
	while(k){
		if(k & 1) ans = 1LL* ans * a % MOD;
		a = 1LL* a * a % MOD;
		k >>= 1;
	}
	return ans;
}

void solve(){
	scanf("%d", &n);
	for(int i = 1; i <= n; i++) scanf("%d%d", &x[i], &y[i]);
	f[0] = 1LL* y[1] * qmi(y[1] - x[1], MOD - 2) % MOD;
	s[0] = f[0];
	for(int i = 1; i < n; i++){
		f[i] = (1LL* x[i + 1] * s[i - 1] % MOD + y[i + 1]) % MOD * qmi(y[i + 1] - x[i + 1], MOD - 2) % MOD;
		s[i] = (1LL* s[i - 1] + f[i]) % MOD;
	}
	for(int i = 0; i < n; i++) {
		ans = (1LL* ans + f[i]) % MOD;
	}
	printf("%d\n", ans);
}

int main(){
	int T = 1;
//	scanf("%d", &T);
	while(T -- ){
		solve();
	}
	return 0;
}

2.2、完全图

  一个 $n$ 个点的完全图，求从 $S$ 走到 $T$ 的期望时间。

3、常见的期望DP模型

  期望题目的关键，从后往前推，即 $DP$ 状态 $f[i]$ 表示定义成从 $i$ 到 $n$ 的期望。（直接建图 + 记忆化搜索) / 直接递推。或者建反图 + $topsort$。

  ① 定义 $DP$ 状态。
  ② 推导期望递推式。

应用题目：

《绿豆蛙的归宿》

方法1： 正向图 + 记忆化搜索（递归到最后面，然后返回来）

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 100010, M = 2 * N;
int h[N], e[M], ne[M], w[M], idx;
double f[N];  //f[i]表示i的后续结点的期望总和
int dout[N];
int n, m;

void add(int a, int b, int c){
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

double dp(int u){
    if(f[u] >= 0) return f[u];  //记忆化搜索
    f[u] = 0;
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        f[u] += (double)(w[i] + dp(j)) / dout[u];
    }
    return f[u];
}

int main(){
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while(m -- ){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
        dout[a]++;
    }

    memset(f, -1, sizeof f);
    printf("%.2lf\n", dp(1));

    return 0;
}

方法2： 建反图 + 拓扑排序

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, M = 2 * N;
double f[N];
int h[N], e[M], ne[M], w[M], idx;
int din[N], sdin[N];
int q[N], hh, tt;
int n, m;

void add(int a, int b, int c){
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void topsort(){
    hh = 0, tt = -1;
    q[++tt] = n;
    while(hh <= tt){
        int t = q[hh++];
        for(int i = h[t]; ~i; i = ne[i]){
            int j = e[i];
            f[j] += (f[t] + w[i]) / sdin[j];
            din[j]--;
            if(din[j] == 0) q[++tt] = j;
        }
    }
}

int main(){
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i++){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(b, a, c);  //建反图
        sdin[a]++, din[a]++;
    }
    topsort();
    printf("%.2lf\n", f[1]);

    return 0;
}

《游戏的买》

AC代码：

#include <bits/stdc++.h>
using namespace std;
 
const int N = 100010;
double f[N];
int a[N], b[N];
int n;
 
void solve(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    for(int i = 1; i <= n; i++) scanf("%d", &b[i]);
    f[n] = (a[n] + b[n]) / 2.0;
    for(int i = n - 1; i >= 1; i--){
        f[i] = min(f[i + 1], 1.0 * a[i]) / 2.0 + min(f[i + 1], 1.0 * b[i]) / 2.0;
    }
    printf("%.3lf\n", f[1]);
}
 
 
int main(){
    int T;
    scanf("%d", &T);
    while(T -- ){
        solve();
    }
    return 0;
}

二、连续型随机变量

概率密度函数 $f(x) = \int_{-\infty }^{+\infty}f(x)dx$，满足：

• $P(a, b) = \int_{a}^{b}f(x)dx$。（$x$在范围$a$到$b$的概率为概率密度函数在这上面的积分）
• $\int_{-\infty }^{+\infty}f(x)dx = 1$

最简单的形式为等概率的概率密度函数：如$f(x) = \frac{1}{x}$

连续型随机变量的期望为 $\int_{-\infty }^{+\infty}xf(x)dx$

对应练习
P5104 红包发红包

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int MOD = 1e9 + 7;
LL w, n, k;

int qmi(int a, LL k){
	int ans = 1;
	while(k){
		if(k & 1) ans = 1LL* ans * a % MOD;
		a = 1LL* a * a % MOD;
		k >>= 1; 
	}
	return ans;
}

void solve(){
	scanf("%lld%lld%lld", &w, &n, &k);
	int v = qmi(2, k);
	printf("%d\n", w * qmi(v, MOD - 2) % MOD);
}

int main(){
	int _ = 1;
//	scanf("%d", &_);
	while( _ -- ){
		solve();
	}
	return 0;
}