随着第六场的结束,这场短暂的旅行也走到了终点。虽然依旧很cai,但是cai并快乐着~
1、B题《阿宁的倍数》
题目描述
阿宁有一个长度为 的数组 ,下标从 开始,有 次操作。
修改操作:数组末尾增加一个数 ,数组长度加 。
询问操作:有多少个 ,满足 是 的倍数?
输入描述
第一行两个整数 。
第二行 个整数 。
接下来 行,每行两个数 ,代表一次操作。
如果 是 代表是修改操作;如果是 代表是询问操作。
保证至少有一次询问操作。
如果是修改操作,。
如果是询问操作, 小于等于当前数组长度。
输出描述
对于每次询问操作,输出一个整数,占一行。
示例1
输入:
5 5
2 4 1 5 6
2 1
1 5
1 1
2 3
2 4
输出:
2
4
1
说明
询问操作, 是 的倍数。
修改操作,数组变成 。
修改操作,数组变成 。
询问操作, 是 的倍数。
询问操作, 是 的倍数。
分析
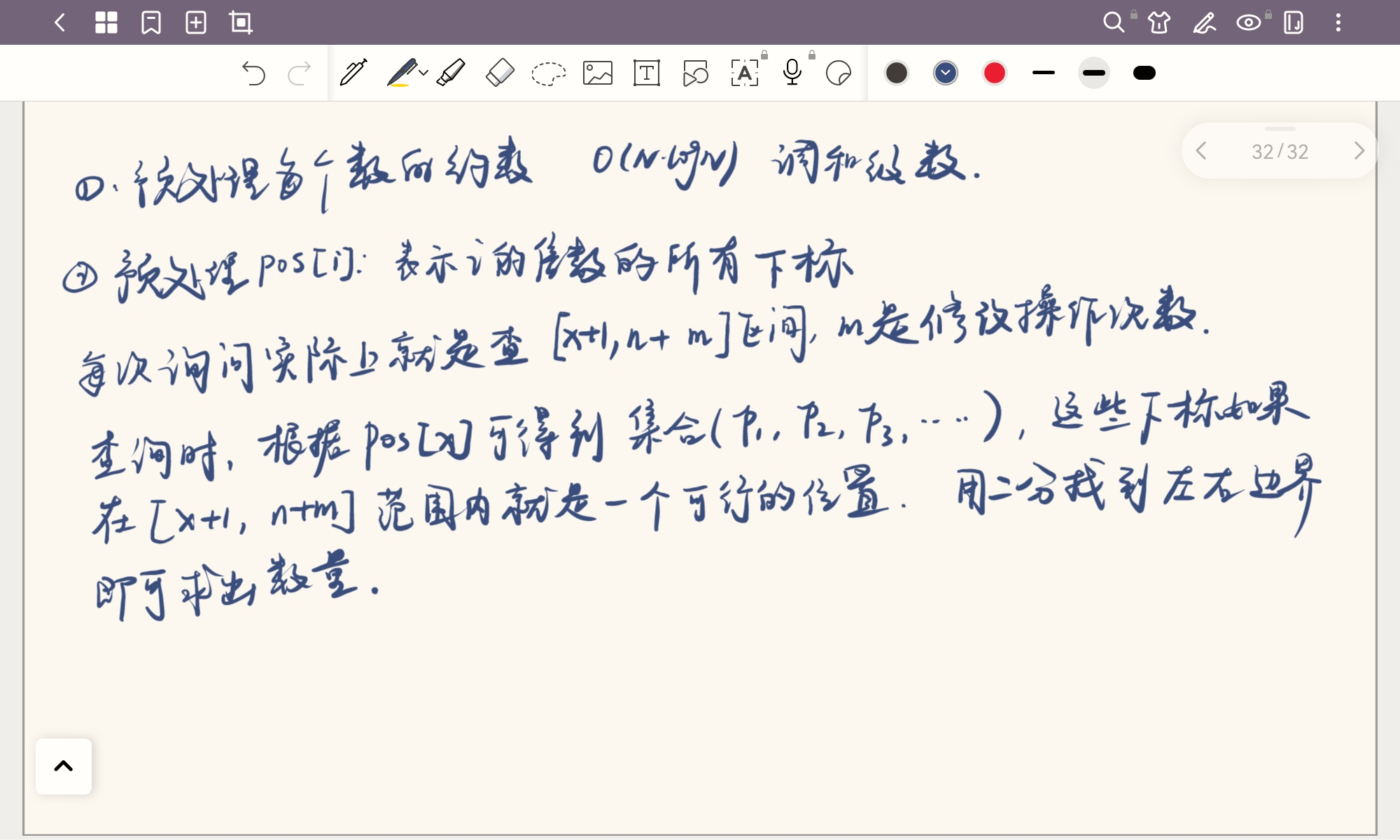
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N = 4e5 + 10;
int a[N];
vector<int> fact[N], pos[N];
int n, m;
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
//预处理约数
for(int i = 1; i <= 200000; i++)
for(int j = 1; j <= 200000 / i; j++)
fact[i * j].push_back(i);
//预处理pos[]
for(int i = 1; i <= n; i++)
for(int j = 0; j < fact[a[i]].size(); j++){ //a[i]的所有约数
int x = fact[a[i]][j];
pos[x].push_back(i); //i下标位置的数是x的倍数
}
while(m -- ){
int op, x;
scanf("%d%d", &op, &x);
if(op == 1){ //x是值
a[++n] = x;
for(int i = 0; i < fact[x].size(); i++){
int y = fact[x][i];
pos[y].push_back(n);
}
}
else{ //x是下标
int l = 0, r = pos[a[x]].size() - 1;
//找到大于等于x + 1的第一个位置和小于等于n的最后一个位置
int lidx = 0, ridx = 0;
while(l < r){
int mid = l + r >> 1;
if(pos[a[x]][mid] >= x + 1) r = mid;
else l = mid + 1;
}
if(pos[a[x]][l] >= x + 1) lidx = l; //可能移动到最右边
else{
printf("%d\n", 0);
continue;
}
l = 0, r = pos[a[x]].size() - 1;
while(l < r){
int mid = l + r + 1 >> 1;
if(pos[a[x]][mid] <= n) l = mid;
else r = mid - 1;
}
ridx = l;
// if(pos[a[x]][l] <= n) ridx = l;
// else{
// printf("%d\n", 0);
// continue;
// }
printf("%d\n", ridx - lidx + 1);
}
}
return 0;
}
2、D题《阿宁的毒瘤题》
阿宁的毒瘤题
题目描述
阿宁被鉴定成毒瘤出题人。
一个长度为 且仅有小写字母的字符串 ,阿宁的毒瘤程度为 串的"udu"子序列的个数。
现在阿宁痛心疾首,想降低毒瘤程度。
阿宁想修改其中 串的一个字符(也可以不修改。只能修改成小写字母),需要修改后毒瘤程度最小。
子序列:指按照原串的顺序取一些字符,组成新的字符串。例如"dudu"、“udu"是"dudovoudu"的子序列,而"uudd”、"abc"不是。
阿宁想知道修改后的 是什么?
输入描述
一个仅包含小写字母的字符串 。
输出描述
输出修改后的 串。
如果答案有多个,输出任意一解即可。
示例1
输入:
dudovoudu
输出:
dddovoudu
说明
"dudovoudu"有 个"udu"子序列,分别是 , , , 。
"dddovoudu"有 个"udu"子序列,是 。
分析
前缀和模拟即可,具体细节见代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
LL scu[N], c_ud[N], cf_du[N];
string s;
/**
错误原因:c_ud和cf_du不能用前缀和的形式来计算后半段的ud、du数量,
因为前半段中的u和后半段中的d是有耦合的。
正确统计后半段du数量的方法为从后往前扫描来统计。
*/
int main(){
cin >> s;
int n = s.size();
s = ' ' + s;
//预处理
for(int i = 1; i <= n; i++) {
scu[i] = scu[i - 1] + (s[i] == 'u');
}
//正向统计ud数量
int cntu = 0;
for(int i = 1; i <= n; i++){
if(s[i] == 'u') cntu++;
c_ud[i] = c_ud[i - 1] + (s[i] == 'd' ? cntu : 0);
}
//反向统计du数量
cntu = 0;
for(int i = n; i >= 1; i--){
if(s[i] == 'u') cntu++;
cf_du[i] = cf_du[i + 1] + (s[i] == 'd' ? cntu : 0);
}
LL maxv = 0; //最多削减的数量
int idx = 1;
for(int i = 1; i <= n; i++){
if(s[i] == 'd'){
LL lc = scu[i - 1], rc = scu[n] - scu[i];
if(lc * rc > maxv){
maxv = lc * rc;
idx = i;
}
}
else if(s[i] == 'u'){
LL llc = c_ud[i - 1], rrc = cf_du[i + 1];
if(llc + rrc > maxv){
maxv = llc + rrc;
idx = i;
}
}
}
s[idx] = 'a';
cout << s.substr(1) << endl;
return 0;
}
3、E题《阿宁的生成树》
阿宁的生成树
题目描述
阿宁有一个 个节点的完全图,编号从 到 。对于点 和点 ,如果 ,那么 和 之间有一条边权为 的边,否则有一条边权为 的边。
阿宁想求出该完全图的最小生成树。
输入描述
输入两个整数 。
输出描述
一个整数,表示最小生成树的边权和。
示例1
输入:
5 3
输出:
10
说明
其中的一个最小生成树:
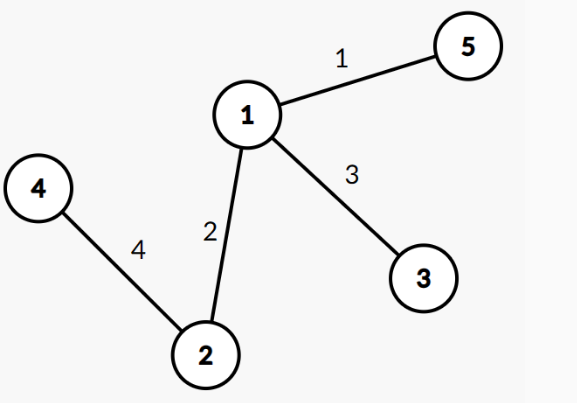
分析

AC代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n, k;
LL ans;
int gcd(int a, int b){
return b ? gcd(b, a % b) : a;
}
int main(){
scanf("%d%d", &n, &k);
int num = min(n, k + 1);
ans = n - num; //从k + 2到n的数量
for(int i = 2; i <= num; i++){
int cur = i; //lcm(1, cur) = i是lcm情况下的最小值
for(int j = i + k + 1; j <= n; j++){
cur = min(cur, gcd(i, j));
if(cur == 1) break;
}
ans += cur;
}
printf("%lld\n", ans);
return 0;
}
I题《阿宁前往沙城》
阿宁前往沙城
题目描述
沙城中有 个城市,它的主宰沙神住在第 号城市。
沙神将要在第 号城市举办宴会。作为沙神的尘民阿宁,为了膜拜、歌颂沙神,将要从 号城市前往 号城市参加宴会。
沙神的尘民们都一个“沙卷”技能,阿宁也有这个技能:选择两条道路,使其中一条道路的通过时间变为 ,并毁灭另一条道路。被毁灭的道路无法通行,且无法被“沙卷”技能选择。
阿宁可以在任何时候使用任意次“沙卷”,使用“沙卷”不消耗时间。
为了不错过沙神的宴会,阿宁想要尽快到达 号城市。最少需要多少时间才能到达 号城市?
输入描述
第一行两个整数 。
接下来 行,每行三个整数 ,表示 号城市和 号城市有道路相连,通过该道路需要 的时间(道路是双向的)。
保证在使用“沙卷”之前, 号城市能到达 号城市。
输出描述
输出一个整数,表示阿宁从 号城市到达 号城市的最短时间。
示例1
输入:
5 6
1 2 4
2 3 1
2 4 5
5 3 4
4 5 1
5 5 1
输出:
3
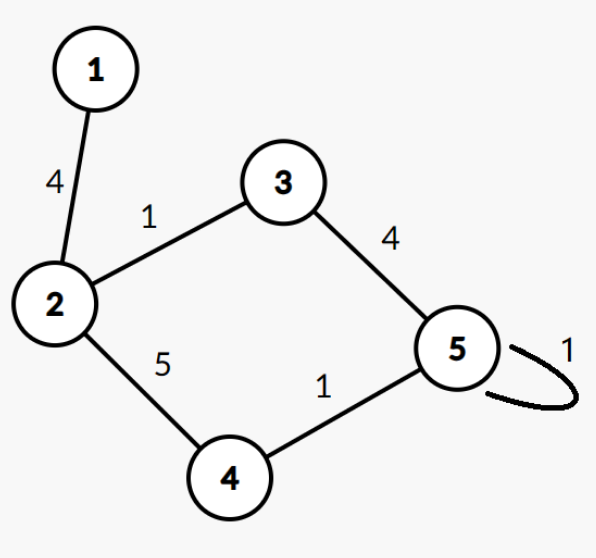
说明
使用“沙卷”使 道路的通过时间变成 ,破环 道路。
从 号城市走到 号城市,耗费时间 。
从 号城市走到 号城市,耗费时间 。
使用“沙卷”使 道路的通过时间变成 ,破环 道路。
从 号城市走到 号城市,耗费时间 。
示例2
输入:
2 1
1 2 3
输出:
3
分析
+ 贪心
贪心思想:每经过一条边,在之后就可以把这条边毁灭,然后把后一条路径变为 。
这样如果 ,那么说明第一条边无法变为 。否则如果 ,那么从 号点到 号点的路径中每一段权值都可以变成 。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int h[N], e[2 * N], ne[2 * N], w[2 * N], idx;
int q[N], hh, tt;
int dist[N];
int n, m;
int minv = 1e9;
void add(int a, int b, int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void bfs(){
hh = 0, tt = -1;
memset(dist, -1, sizeof dist);
q[++tt] = 1;
dist[1] = 0;
while(hh <= tt){
auto t = q[hh++];
for(int i = h[t]; ~i; i = ne[i]){
int j = e[i];
if(dist[j] == -1){
dist[j] = dist[t] + 1;
q[++tt] = j;
}
}
}
}
int main(){
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
for(int i = 0; i < m; i++){
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
//当1号点连着多条边时,dist[n]一定小于m,此时结果是dist[n],与minv无关。
if(a == 1 || b == 1){
minv = c; //最小起始边
}
}
bfs();
if(dist[n] == m) printf("%d\n", (m == 1) ? minv : (minv + dist[n] - 1));
else printf("%d\n", dist[n]);
return 0;
}