牛客小白月赛67——F题《翼伯父作威》

题目链接

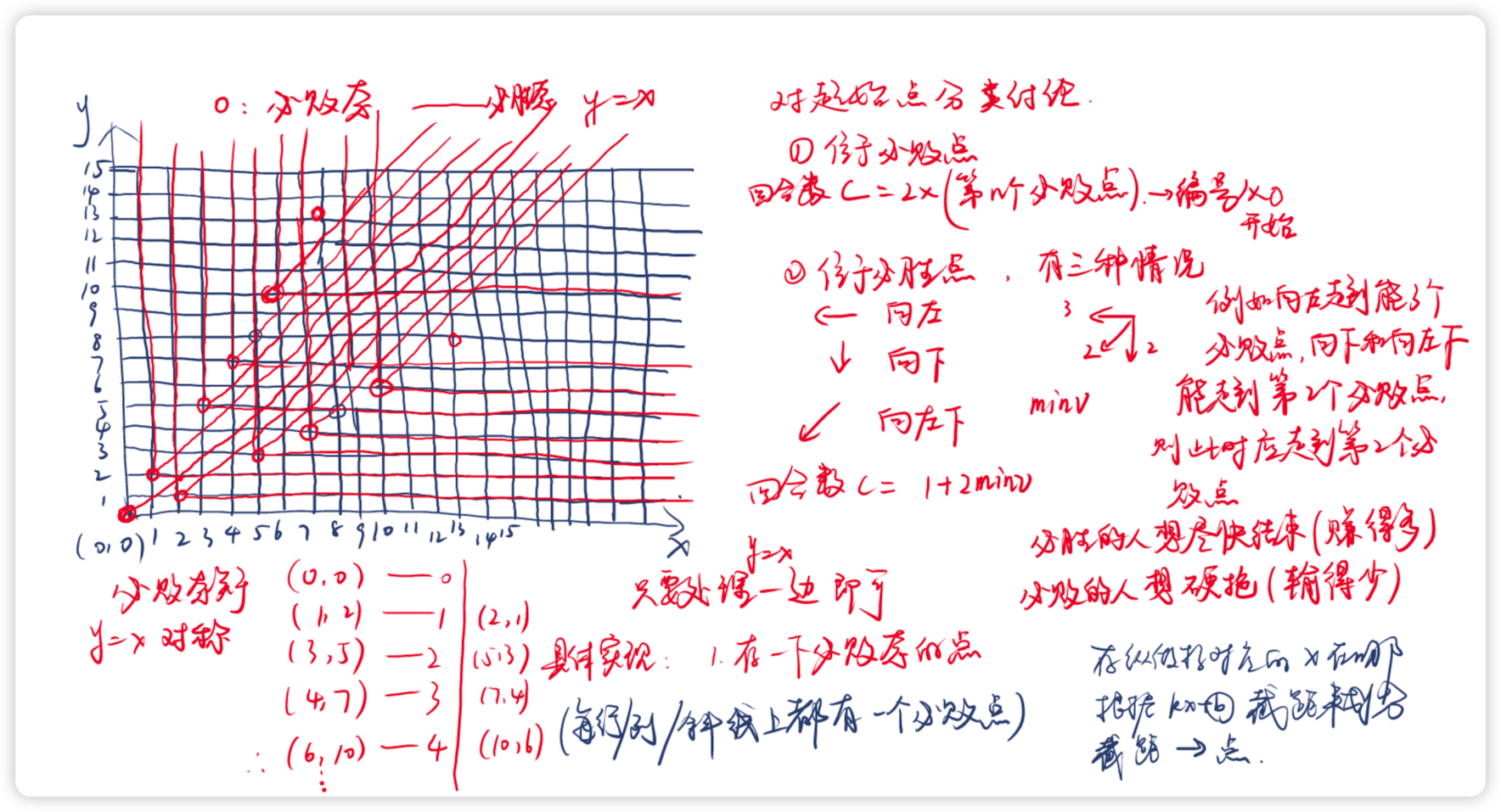
博弈论——威佐夫博弈

• 必败态的所有下一状态都是必胜态；
• 必胜态的下一状态之一必有必败态。

#include <bits/stdc++.h>
using namespace std;

#define fs first
#define sc second
typedef pair<int, int> PII;
const int N = 1000000;
bool st[N + 10];
int mp1[N + 10]; //坐标映射
PII mpk[N + 10]; //y = kx + b, 由斜率映射到点, 根据截距来划分，表示截距为b的直线上的必败点坐标
int x, y;

//计算必败点
void calc(){
	int d = 1;
	for(int i = 1; i <= N; i++){
		if(!st[i] && i + d <= N){
			st[i] = true, st[i + d] = true;
			mp1[i] = i + d;  
			mp1[i + d] = i;
			mpk[d] = {i, i + d}; //存y = x上半部分即可
			d++;
		}
	}
}

void solve(){
	scanf("%d%d", &x, &y);
	//只考虑y = x的上半部分即可-- y >= x
	if(x > y) swap(x, y);
	int step = 0;
	if(mp1[x] == y) step = 2 * abs(x - y);
	else{  //位于必胜态
		//必败点的编号可以根据abs(x - y)来求出
		int mn = 1e9;
		//往左走--需要满足x > nx, 此时左边必败点的坐标为(nx, y)
		int nx = mp1[y];
		if(nx && x > nx) {
			mn = min(mn, 2 * abs(nx - y));
		}
		//往下走--需要满足y > ny, 下方必败点的坐标为(x, ny)
		int ny = mp1[x];  //x = x直线上的必败点的纵坐标
		if(ny && y > ny) {
			mn = min(mn, 2 * abs(ny - x));
		}
		auto pt = mpk[abs(y - x)];  
		if(x > pt.fs && y > pt.sc) {  //在同一条直线上，所以截距相等
			mn = min(mn, 2 * abs(x - y));
		}
		step = 1 + mn;
	}
	printf("%d\n", 2000000000 - step);
}


int main(){
	int T;
	scanf("%d", &T);
	calc();
	while(T -- ){
		solve();
	}
	return 0;
}

PS: 之前不知道为什么用一个数组id存储是第几个必败点的方式过不了，晚上改了改能过了。。。皆大欢喜hh

#include <bits/stdc++.h>
using namespace std;

#define fs first
#define sc second
typedef pair<int, int> PII;
const int N = 1000000;
bool st[N + 10];
int mp1[N + 10]; //坐标映射
int id[N + 10];
PII mpk[N + 10]; //y = kx + b, 由斜率映射到点, 根据截距来划分，表示截距为b的直线上的必败点坐标
int x, y;

//计算必败点
void calc(){
	int d = 1;
	for(int i = 1; i <= N; i++){
		if(!st[i] && i + d <= N){
			st[i] = true, st[i + d] = true;
			mp1[i] = i + d;  
			mp1[i + d] = i;
			id[i] = id[i + d] = d;
			mpk[d] = {i, i + d}; //存y = x上半部分即可
			d++;
		}
	}
}

void solve(){
	scanf("%d%d", &x, &y);
	//只考虑y = x的上半部分即可-- y >= x
	if(x > y) swap(x, y);
	int step = 0;
	if(mp1[x] == y) step = 2 * id[x];
	else{  //位于必胜态
		//必败点的编号可以根据abs(x - y)来求出
		int mn = 1e9;
		//往左走--需要满足x > nx, 此时左边必败点的坐标为(nx, y)
		int nx = mp1[y];
		if(nx && x > nx) {
			mn = min(mn, 2 * id[nx]);
		}
		//往下走--需要满足y > ny, 下方必败点的坐标为(x, ny)
		int ny = mp1[x];  //x = x直线上的必败点的纵坐标
		if(ny && y > ny) {
			mn = min(mn, 2 * id[mp1[ny]]);
		}
		auto pt = mpk[abs(y - x)];  
		if(x > pt.fs && y > pt.sc) {  //在同一条直线上，所以截距相等
			mn = min(mn, 2 * abs(x - y));
		}
		step = 1 + mn;
	}
	printf("%d\n", 2000000000 - step);
}


int main(){
	int T;
	scanf("%d", &T);
	calc();
	while(T -- ){
		solve();
	}
	return 0;
}