莫队算法

学习了一下莫队算法，ORZ

  莫队，是莫涛发明的一种解决区间查询等问题的离线算法，基于分块思想，复杂度为$O(n\sqrt{n})$。本文只涉及普通莫队。

  一般来说，如果可以在 $O(1)$时间内从 $[l, r]$ 的答案转移到 $[l - 1, r]$、 $[l + 1, r]$、$[l, r - 1]$ 、$[l, r + 1]$ 这四个与之紧邻的区间的答案，则可以考虑使用莫队。

  典型应用是给出若干个查询，问区间中有多少个不同的数。

  莫队算法优化的核心是分块和排序。我们将大小为n的序列分为$\sqrt{n}$块，从1到$\sqrt{n}$编号，然后根据这个对查询区间进行排序。一种方法是把查询区间按照左端点所在块的序号排个序，如果左端点所在块相同，再按右端点排序（根据右端点进行奇偶排序）。排完序后我们再进行左右指针跳来跳去的操作，虽然看似没多大用，但带来的优化实际上极大。

特别注意： l, r 的初始值为l = 1, r = 0, 然后存数下标从1开始。

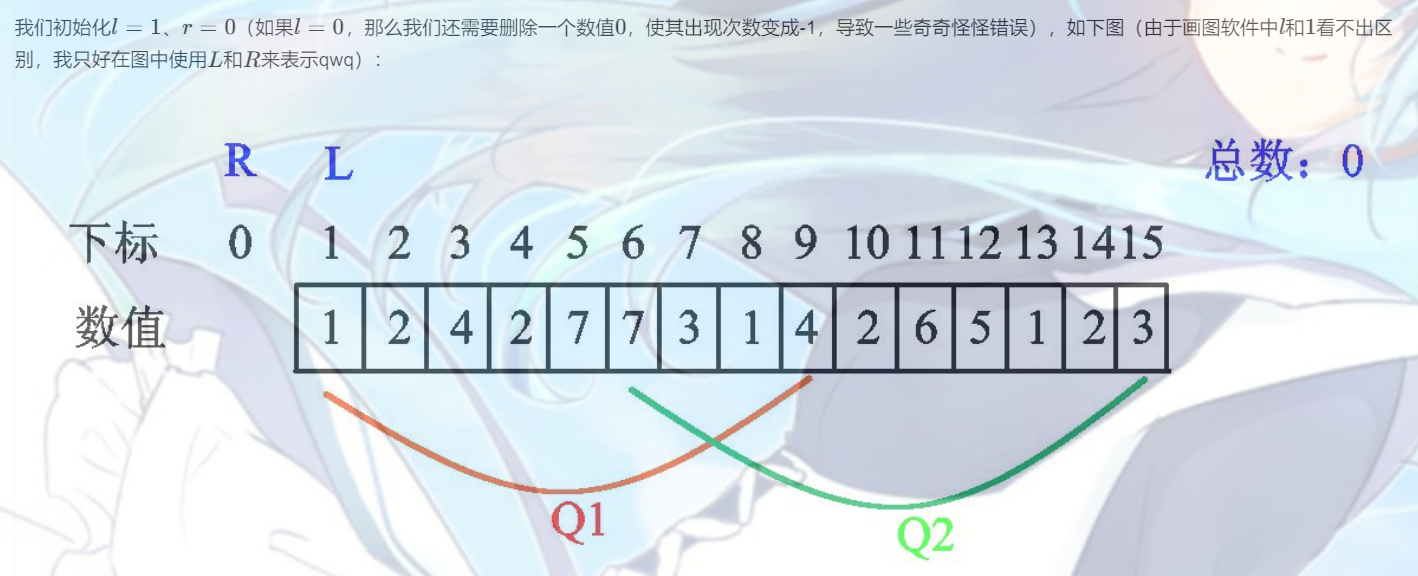
具体讲解：=======>Pecco大佬

关于莫队分块以及奇偶优化的详细证明：=======>WAMonster大佬

应用：

记录一下莫队板子~

DQUERY - D-query

#include <bits/stdc++.h>
using namespace std;

const int N = 30010, M = 200010, MAXN = 1e6 + 10;
int sq;
struct Query{
	int l, r, id;
	bool operator< (const Query& t) const{
		if(l / sq != t.l / sq) return l < t.l;
		if(l / sq & 1) return r < t.r;
		return r > t.r;
	}
}q[M];
int cur, n, m;
int a[N], cnt[MAXN], res[M];

void add(int p){
	cnt[a[p]]++;
	if(cnt[a[p]] == 1) cur++;
}

void del(int p){
	--cnt[a[p]];
	if(cnt[a[p]] == 0) cur--;
}

void solve(){
	scanf("%d", &n);
	sq = sqrt(n);
	for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
	scanf("%d", &m);
	for(int i = 1; i <= m; i++){
		int l, r;
		scanf("%d%d", &l, &r);
		q[i] = {l, r, i};
	}
	sort(q + 1, q + 1 + m);
	int l = 1, r = 0;  //初始值, 下标从1开始 
	for(int i = 1; i <= m; i++){
		while(l > q[i].l) add(--l);
		while(r < q[i].r) add(++r);
		while(l < q[i].l) del(l++);
		while(r > q[i].r) del(r--);
		res[q[i].id] = cur;
	}
	for(int i = 1; i <= m; i++) printf("%d\n", res[i]);
} 

int main(){
	int T = 1; 
//	scanf("%d", &T);
	while(T -- ){
		solve();
	}
} 

重复的数

AC代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;
int sq;
struct Query{
	int l, r, id, k;
	bool operator< (const Query& t) const{
		if(l / sq != t.l / sq) return l < t.l;
		if(l / sq & 1) return r < t.r;
		return r > t.r;
	}
}q[N];
int n, m;
int a[N], s[N], cnt[N]; //s[x]表示出现x出现了几次，cnt[x]表示区间内出现x次的数有几个 
int res[N];

void add(int p){
	cnt[s[a[p]]]--;
	cnt[++s[a[p]]]++;
}

void del(int p){
	cnt[s[a[p]]]--;
	cnt[--s[a[p]]]++;
}

void solve(){
	scanf("%d", &n);
	sq = sqrt(n);
	for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
	scanf("%d", &m);
	for(int i = 1; i <= m; i++){
		int l, r, k;
		scanf("%d%d%d", &l, &r, &k);
		q[i] = {l, r, i, k};
	}
	sort(q + 1, q + 1 + m);
	int l = 1, r = 0;
	for(int i = 1; i <= m; i++){
		while(l > q[i].l) add(--l);
		while(r < q[i].r) add(++r);
		while(l < q[i].l) del(l++);
		while(r > q[i].r) del(r--);
		res[q[i].id] = cnt[q[i].k];	
	}
	for(int i = 1; i <= m; i++) printf("%d\n", res[i]);
}

int main(){
	int T = 1;
//	scanf("%d", &T);
	while(T -- ){
		solve();
	}
	return 0;
}