启发式合并与树链剖分

启发式合并

[HNOI2009] 梦幻布丁 - 洛谷

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;
int now[N], a[N];
vector<int> g[N];
int n, m, ans;

void _merge(int x, int y){
	for(auto i : g[x]){
		if(a[i - 1] == y) ans--;
		if(a[i + 1] == y) ans--; 
	}
	for(auto i : g[x]) a[i] = y;
	for(auto i : g[x]) g[y].push_back(i);
	g[x].clear();
}

void solve(){
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
		now[a[i]] = a[i];
		if(a[i] != a[i - 1]) ans++;
		g[a[i]].push_back(i); 
	}
	int op, x, y;
	while(m -- ){
		scanf("%d", &op); 
		if(op == 2) printf("%d\n", ans);
		else{
			scanf("%d%d", &x, &y);  
			if(x == y) continue;
			if(g[now[x]].size() > g[now[y]].size()) swap(now[x], now[y]);
			_merge(now[x], now[y]);
		}
	} 
}

int main(){
	int _ = 1;
	while(_ -- ) solve();
	return 0;
} 

看董晓算法

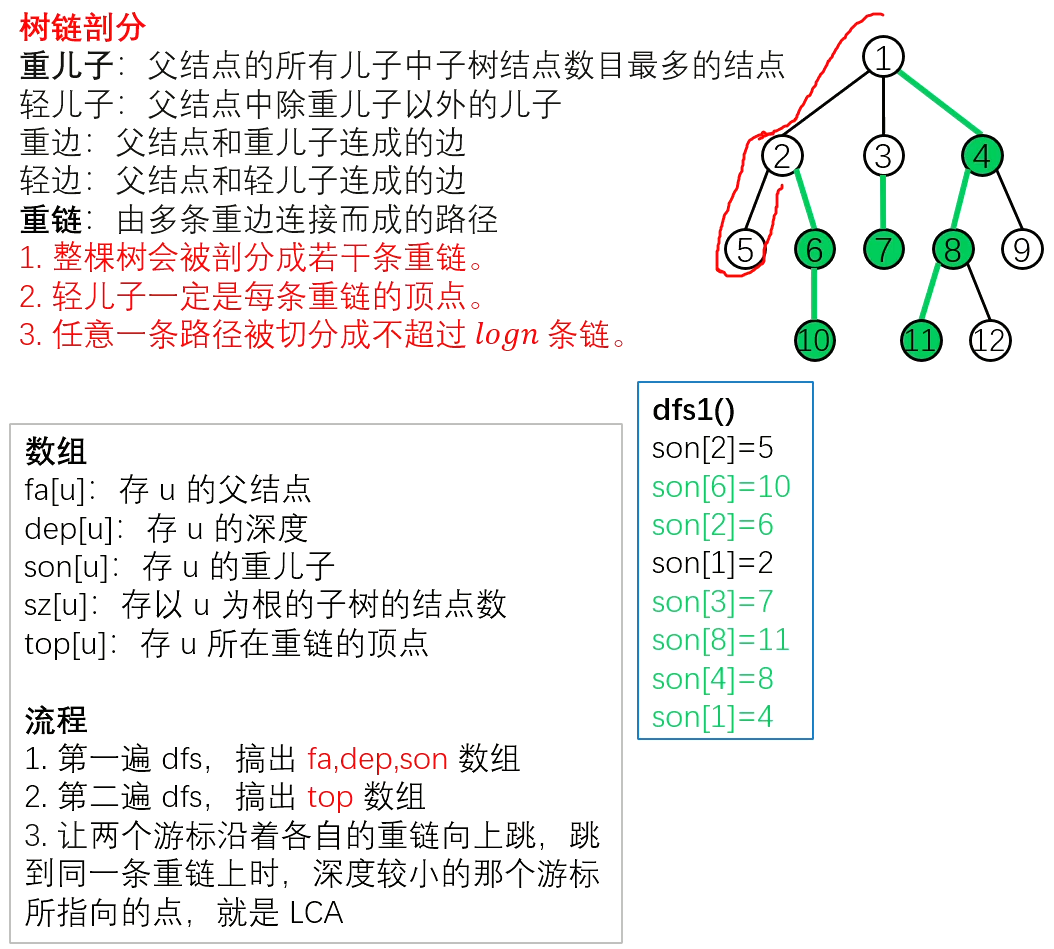
树链剖分求LCA

祖孙询问

#include <bits/stdc++.h>
using namespace std;

const int N = 40010;
int h[N], e[2 * N], ne[2 * N], idx;
int fa[N], sz[N], dep[N], hson[N], top[N];
int n, m, root;

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs1(int u, int p, int d){
    int size = 1, ma = 0;
    dep[u] = d;
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if(j == p) continue;
        dfs1(j, u, d + 1);
        fa[j] = u;
        size += sz[j];
        if(sz[j] > ma) hson[u] = j, ma = sz[j];
    }
    sz[u] = size;
}

void dfs2(int u){
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if(!top[j]){
            if(j == hson[u]) top[j] = top[u];
            else top[j] = j;
            dfs2(j);
        }
    } 
}

//最终会走到同一条重链上 
int lca(int a, int b){
    while(top[a] != top[b]){
        if(dep[top[a]] > dep[top[b]]) a = fa[top[a]];
        else b = fa[top[b]];
    }
    return (dep[a] > dep[b] ? b : a);
}

void solve(){
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for(int i = 0; i < n; i++){
        int a, b; scanf("%d%d", &a, &b);
        if(b == -1) root = a;
        else add(a, b), add(b, a);
    }
    top[root] = root;   //根结点赋值很重要！
    dfs1(root, -1, 1);
    dfs2(root);
    scanf("%d", &m);
    while(m -- ){
        int x, y; scanf("%d%d", &x, &y);
        int p = lca(x, y);
        if(p == x) puts("1");
        else if(p == y) puts("2");
        else puts("0"); 
    }
}

int main(){
    int _ = 1;
    while(_ -- ) solve();
    return 0;
} 

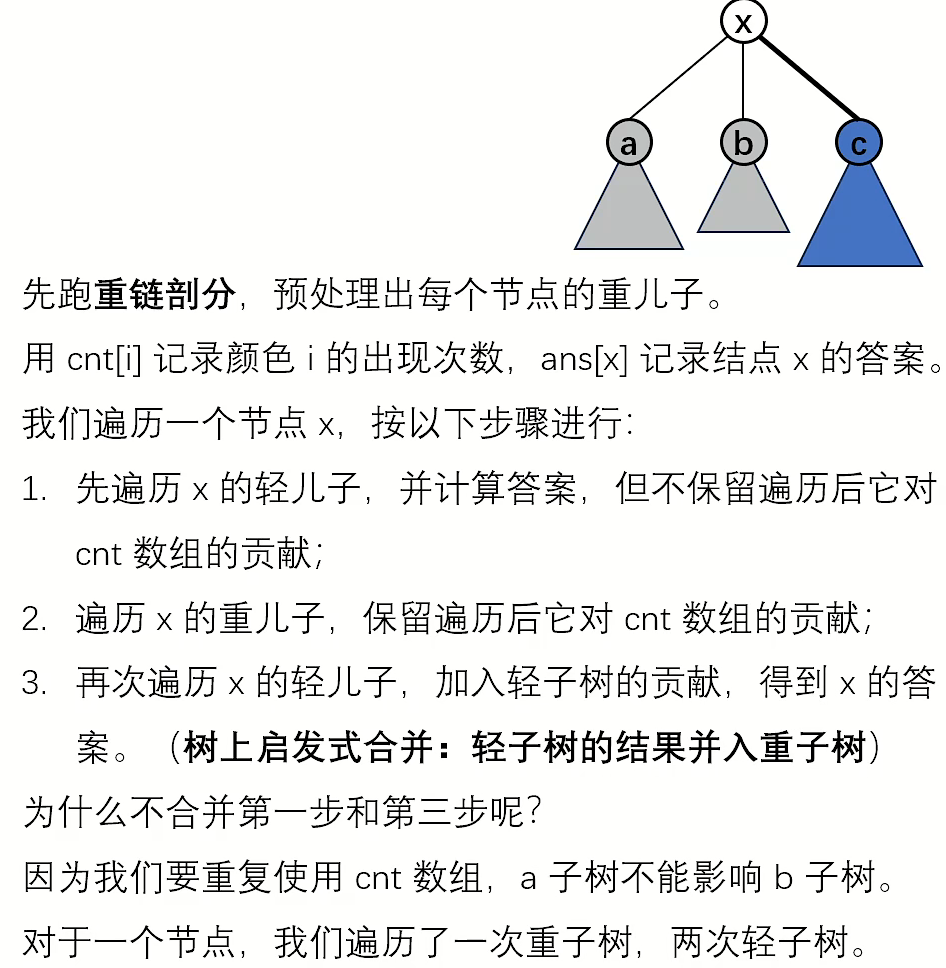
树上启发式合并（DSU on Tree）

https://zhuanlan.zhihu.com/p/565967113

E. Lomsat gelral

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 100010;
int h[N], e[2 * N], ne[2 * N], idx;
int col[N];
LL sum, res[N];
int fa[N], sz[N], dep[N], hson[N], cnt[N], mx;  
int n, m, root;

void add(int a, int b){
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void _add(int u, int fa, int son){
	cnt[col[u]]++;
	if(cnt[col[u]] > mx) mx = cnt[col[u]], sum = col[u];
	else if(cnt[col[u]] == mx) sum += col[u];
	for(int i = h[u]; ~i; i = ne[i]){
		int j = e[i];
		if(j != fa && j != son) _add(j, u, son);   //重子树不加，因为在上一层中没有减去 
	} 
}

void _sub(int u, int fa){
	cnt[col[u]]--;
	for(int i = h[u]; ~i; i = ne[i]){
		int j = e[i];
		if(j != fa) _sub(j, u);
	}
} 

//树链剖分只搜出重儿子即可 
void dfs1(int u, int p, int d){
	int size = 1, ma = 0;
	for(int i = h[u]; ~i; i = ne[i]){
		int j = e[i];
		if(j == p) continue;
		dfs1(j, u, d + 1);
		fa[j] = u;
		size += sz[j];
		if(sz[j] > ma) hson[u] = j, ma = sz[j];		
	}
	sz[u] = size;
}

void dfs2(int u, int fa, int opt){
	for(int i = h[u]; ~i; i = ne[i]){   //先搜轻儿子 
		int j = e[i]; 
		if(j != fa && j != hson[u]) dfs2(j, u, 0); 
	}
	if(hson[u]) dfs2(hson[u], u, 1);   //后搜重儿子
	_add(u, fa, hson[u]);   //累加x和轻子树贡献（因为在上一层中被减去了） 
	res[u] = sum;    //存储答案 
	if(!opt) _sub(u, fa), sum = mx = 0;  //减掉轻子树贡献 
}
 
void solve(){
	scanf("%d", &n);
	for(int i = 1; i <= n; i++) scanf("%d", &col[i]);
	memset(h, -1, sizeof h);
	for(int i = 0; i < n - 1; i++){
		int x, y; scanf("%d%d", &x, &y);
		add(x, y), add(y, x); 
	}
	dfs1(1, -1, 1);
	dfs2(1, -1, 0);
	for(int i = 1; i <= n; i++) printf("%lld%c", res[i], " \n"[i == n]);
}

int main(){
	int _ = 1;
	while(_ -- ) solve();
	return 0;
}