D题 =====>《Difference》
第k大(二分)+ 双指针 + ST表,细节巨多,折磨王。。。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 500010;
int mx[N][21], mn[N][21], Log2[N];
int a[N], n;
LL k, ans;
//ST
void ST(){
for(int i = 2; i <= n; i++) Log2[i] = Log2[i / 2] + 1;
for(int j = 0; j < 21; j++){
for(int i = 1; i + (1 << j) - 1 <= n; i++){
if(!j) mx[i][j] = mn[i][j] = a[i];
else{
mx[i][j] = max(mx[i][j - 1], mx[i + (1 << j - 1)][j - 1]);
mn[i][j] = min(mn[i][j - 1], mn[i + (1 << j - 1)][j - 1]);
}
}
}
}
int qmx(int l, int r){
int k = Log2[r - l + 1];
return max(mx[l][k], mx[r - (1 << k) + 1][k]);
}
int qmn(int l, int r){
int k = Log2[r - l + 1];
return min(mn[l][k], mn[r - (1 << k) + 1][k]);
}
//窗口具有单调性,因此用双指针
bool check(LL x){
LL res = 0;
for(int i = 1, j = 1; i <= n; i++){
while(j <= i && (1LL* (qmx(j, i) - qmn(j, i)) * (i - j + 1)) >= x) j++;
res += i - j + 1;
}
res++;
return res <= k;
}
void solve(){
scanf("%d%lld", &n, &k);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
ST();
k = 1LL* n * (1 + n) / 2 - k + 1; //转为第k小,方便双指针考虑
LL l = 0, r = 1LL* n * (qmx(1, n) - qmn(1, n));
//二分这里卡了好久
/**
因为双指针找的是小于x的数量,因此二分x时,x越小,得到的统计值ans越小,此时ans <= k越容易满足,
因此二分的是左半段的右边界。
*/
while(l < r){
LL mid = l + r + 1 >> 1;
if(check(mid)) l = mid;
else r = mid - 1;
}
printf("%lld\n", l);
}
int main(){
int _ = 1;
while(_ -- ) solve();
return 0;
}
F题 =====>《K-th Power》
容斥原理

根据容斥原理特点,一般有三种做法:
- 数据量较小时,可用状压方式枚举 AcWing 890. 能被整除的数
- dfs搜索
- 莫比乌斯函数
一:dfs方式
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e7 + 10;
LL primes[N], cnt;
LL qs[N];
bool st[N];
LL l, r, k, res;
void init(int n){
for(int i = 2; i <= n; i++){
if(!st[i]) primes[cnt++] = i;
for(int j = 0; primes[j] <= n / i; j++){
st[primes[j] * i] = true;
if(i % primes[j] == 0) break;
}
}
}
LL qmi(LL a, LL b, LL r){
LL s = 1;
while(b){
if(b & 1) {
if(s > r / a) return 0;
s *= a;
}
if(a > r / a && b >> 1) return 0;
a *= a;
b >>= 1;
}
return s;
}
//做容斥
void dfs(LL x, LL y, int c, int ns){
if(ns & 1) res += x / y;
else if(ns > 0) res -= x / y;
for(int i = c; i < cnt; i++){
if(qs[i] && qs[i] <= x / y){
dfs(x, y * qs[i], i + 1, ns + 1);
}
else break;
}
}
LL calc(LL x){
res = 0;
dfs(x, 1, 0, 0);
return x - res;
}
void solve(){
init(N - 1);
scanf("%lld%lld%lld", &l, &r, &k);
for(int i = 0; i < cnt; i++){
qs[i] = qmi(primes[i], k, r);
if(qs[i] == 0) break;
}
printf("%lld\n", calc(r) - calc(l - 1));
}
int main(){
int _ = 1;
// scanf("%d", &_);
while(_ -- ) solve();
}
二. 莫比乌斯函数方式
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e7 + 10;
LL primes[N], mu[N], cnt;
LL qs[N];
bool st[N];
LL l, r, k, res;
void init(int n){
mu[1] = 1;
for(int i = 2; i <= n; i++){
if(!st[i]) primes[cnt++] = i, mu[i] = -1;
for(int j = 0; primes[j] <= n / i; j++){
st[primes[j] * i] = true;
if(i % primes[j] == 0) break;
mu[primes[j] * i] = -mu[i];
}
}
}
LL qmi(LL a, LL b, LL r){
LL s = 1;
while(b){
if(b & 1) {
if(s > r / a) return 0;
s *= a;
}
if(a > r / a && b >> 1) return 0;
a *= a;
b >>= 1;
}
return s;
}
LL calc(LL x){
LL res = 0;
for(int i = 2; i <= 1e7; i++){
LL t = qmi(i, k, x);
if(t == 0) break;
res += x / t * mu[i];
}
return x + res;
}
void solve(){
init(N - 1);
scanf("%lld%lld%lld", &l, &r, &k);
printf("%lld\n", calc(r) - calc(l - 1));
}
int main(){
int _ = 1;
// scanf("%d", &_);
while(_ -- ) solve();
}
H题 =====>《Permutation Counting》
拓扑排序 组合数 树形dp
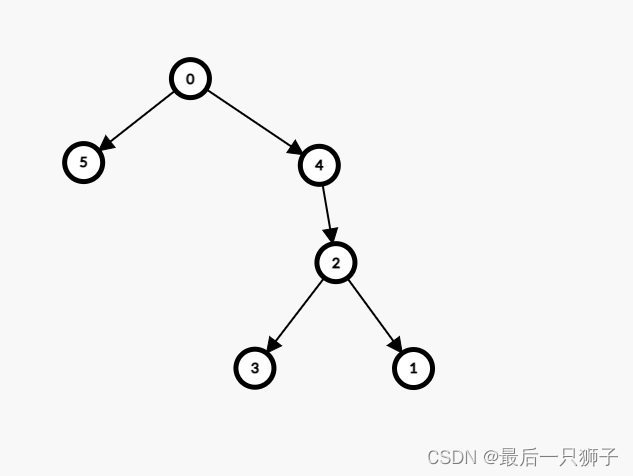
之后发现题目中说明了每对关系(x, y)中x保证不同,假设按照y – > x,说明每个节点都最多只有一个父节点又考虑到是一个有向图且无环,那么就是树形图。原来那种建图方式(x --> y) 表明每个节点可有>1个的父节点。
为了方便计算,可以新建一个虚拟源点0号点,和所有入度为0的点建边。那么就把本题转化为了树上问题。

#include <bits/stdc++.h>
using namespace std;
const int MOD = 998244353, N = 2e6 + 10;
int n, m;
int h[N], e[N], ne[N], idx;
int q[N], hh, tt;
int du[N];
int fact[N], infact[N];
int sz[N], f[N]; //sz[i]代表以i为根的子树的结点数量,注意要设置0号结点作为根结点
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int qmi(int a, int b){
int res = 1;
while(b){
if(b & 1) res = 1LL* res * a % MOD;
a = 1LL* a * a % MOD;
b >>= 1;
}
return res;
}
void init(){
fact[0] = infact[0] = 1;
for(int i = 1; i <= n; i++){
fact[i] = 1LL* fact[i - 1] * i % MOD;
infact[i] = 1LL* infact[i - 1] * qmi(i, MOD - 2) % MOD;
}
}
bool topsort(){
hh = 0, tt = -1;
q[++tt] = 0;
while(hh <= tt){
auto t = q[hh++];
for(int i = h[t]; ~i; i = ne[i]){
int j = e[i];
if(--du[j] == 0){
q[++tt] = j;
}
}
}
return tt == n;
}
int dfs1(int u){
sz[u] = 1;
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
sz[u] += dfs1(j);
}
return sz[u];
}
int dfs2(int u){
f[u] = 1;
int s = sz[u];
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
dfs2(j);
f[u] = 1LL* f[u] * f[j] % MOD * fact[s - 1] % MOD * infact[sz[j]] % MOD
* infact[s - 1 - sz[j]] % MOD;
s -= sz[j];
}
return f[u];
}
void solve(){
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
init();
for(int i = 0; i < m; i++){
int x, y; scanf("%d%d", &x, &y);
add(y, x);
du[x]++;
}
for(int i = 1; i <= n; i++){
if(du[i] == 0) add(0, i), du[i]++;
}
if(topsort()){
dfs1(0);
dfs2(0); //树形dp
printf("%d\n", f[0]);
}
else puts("0");
}
int main(){
int _ = 1;
// scanf("%d", &_);
while(_ -- ) solve();
}